Маятник

Определение "Маятник" в Большой Советской Энциклопедии

Маятники

Маятник, твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси. В физике под Маятник обычно понимают Маятник, совершающий колебания под действием силы тяжести; при этом его ось не должна проходить через центр тяжести тела. Простейший Маятник состоит из небольшого массивного груза C, подвешенного на нити (или лёгком стержне) длиной l. Если считать нить нерастяжимой и пренебречь размерами груза по сравнению с длиной нити, а массой нити по сравнению с массой груза, то груз на нити можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса O (рис. 1, а). Такой Маятник называется математическим. Если же, как это обычно имеет место, колеблющееся тело нельзя рассматривать как материальную точку, то Маятник называется физическим.

Маятники

Математический маятник. Если Маятник, отклоненный от равновесного положения C₀, отпустить без начальной скорости или сообщить точке C скорость, направленную перпендикулярно OC и лежащую в плоскости начального отклонения, то Маятник будет совершать колебания в одной вертикальной плоскости по дуге окружности (плоский, или круговой математический Маятник). В этом случае положение Маятник определяется одной координатой, например углом j, на который Маятник отклонен от положения равновесия. В общем случае колебания Маятник не являются гармоническими; их период T зависит от амплитуды. Если же отклонения Маятник малы, он совершает колебания, близкие к гармоническим, с периодом:
 ,
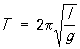где g — ускорение свободного падения; в этом случае период T не зависит от амплитуды, то есть колебания изохронны.

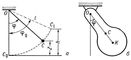
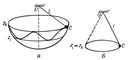
Если отклонённому Маятник сообщить начальную скорость, не лежащую в плоскости начального отклонения, то точка C будет описывать на сфере радиуса l кривые, заключённые между 2 параллелями z = z₁ и z = z₂ (рис. 2, а), где значения z₁ и z₂ зависят от начальных условий (сферический маятник). В частном случае, при z₁ = z₂ (рис. 2, б) точка C будет описывать окружность в горизонтальной плоскости (конический маятник). Из некруговых Маятник особый интерес представляет циклоидальный маятник, колебания которого изохронны при любой величине амплитуды.

Физический маятник. Физическим Маятник обычно называется твёрдое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого Маятник вполне аналогично движению кругового математического Маятник При малых углах отклонения j Маятник также совершает колебания, близкие к гармоническим, с периодом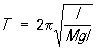
 ,

где I — момент инерции Маятник относительно оси подвеса, l — расстояние от оси подвеса O до центра тяжести C, M — масса Маятник Следовательно, период колебаний физического Маятник совпадает с периодом колебаний такого математического Маятник, который имеет длину l₀ = I/Ml. Эта длина называется приведённой длиной данного физического Маятник

Точка K на продолжении прямой OC, находящаяся на расстоянии l₀ от оси подвеса, называется центром качаний физ. Маятник При этом расстояние OK = l₀ всегда больше, чем OC = l. Точка O оси подвеса Маятник и центр качаний обладают свойством взаимности: если ось подвеса сделать проходящей через центр качаний, то точка O прежней оси подвеса станет новым центром качаний и период колебаний Маятник не изменится. Это свойство взаимности используется в оборотном маятнике для определения приведённой длины l₀; зная l₀ и T, можно найти значение g в данном месте.

Свойствами Маятник широко пользуются в различных приборах: в часах, в приборах для определения ускорения силы тяжести (см. Маятниковый прибор), ускорений движущихся тел, колебаний земной коры (см. Сейсмограф), в гироскопических устройствах, в приборах для экспериментального определения моментов инерции тел и других. См. также Фуко маятник.

  Лит.: Бухгольц Н. Н., Основной курс теоретической механики, ч. 1, Маятник, 1967, § 38, пп. 5, 13, 14; ч. 2, Маятник, 1969, § 12, п. 4; Тарг С. Маятник, Краткий курс теоретической механики, 7 изд., Маятник, 1970, гл. 28, § 155; Хайкин С. Э., Физические основы механики, 2 изд., Маятник, 1971, гл. 13, § 90, 91.
  С. Маятник Тарг.