


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Мера множества
Определение "Мера множества" в Большой Советской Энциклопедии
Мера множества, математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (D) любого квадрата D полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов D1, D2,..., Dn,...; нижнюю грань чисел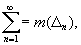
взятую по всевозможным покрытиям множества А, называют верхней (внешней) мерой m*(А) множества А. Нижняя (внутренняя) мера m* (А) множества А определяется как разность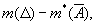
где D - какой-либо квадрат, содержащий множество А, и 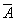 - множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
- множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m (A)D ³ 0; 2) мера суммы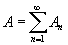
конечной или счётной системы попарно непересекающихся множеств A1, A2..., An... равна сумме их мер: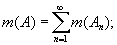
3) при перемещении множества как твёрдого тела его мера не меняется.
Своеобразие понятия «Мера множества» можно пояснить следующим примером: множество А рациональных точек интервала (0, 1) и множество В иррациональных точек того же интервала сходны в том смысле, что каждое из них плотно на интервале (0, 1), т. е., что между любыми двумя точками указанного интервала найдутся как точки множества А, так и точки множества В; в то же время они резко различаются по мере: m (А) = 0, а m (В) = 1.
Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (1898). О других вопросах, связанных с мерой Лебега, см. Интеграл.
Развитие ряда отделов современной математики привело к дальнейшим обобщениям - созданию т. н. абстрактной теории меры. При этом Мера множества определяют аксиоматически. Пусть U - произвольное множество и 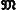 - некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в 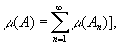
и если, кроме того, система удовлетворяет определённым дополнительным условиям. Множества, входящие в , называют измеримыми (по отношению к мере m). После того как определена мера m, вводят понятие измеримых (по отношению к m) функций и операцию интегрирования.
Многие основные утверждения из теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими видоизменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное в 1933 А. Н. Колмогоровым. Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества U в себя.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. - Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Халмош П. Р., Теория меры, пер. с англ., М., 1953.
Ю. В. Прохоров.
| "БСЭ" >> "М" >> "МЕ" >> "МЕР" >> "МЕРА" |
Статья про "Мера множества" в Большой Советской Энциклопедии была прочитана 1150 раз
| Пицца в сковороде |
| Английский рыбный пирог |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная