


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Неприводимый многочлен
Определение "Неприводимый многочлен" в Большой Советской Энциклопедии
Неприводимый многочлен, многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициентов многочлена. Так, многочлен x3 + 2 неприводим, если в качестве коэффициентов допускать только рациональные числа, но разлагается в произведение двух Неприводимый многочлен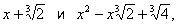
если в качестве коэффициентов брать любые действительные числа, и в произведение трёх множителей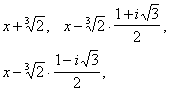
если коэффициентами будут числа комплексные. В общем случае понятие неприводимости определяется для многочленов с коэффициентами, принадлежащими произвольному полю (см. Поле алгебраическое). Часто Неприводимый многочлен называют многочлен с рациональными коэффициентами, не разлагающийся на множители более низкой степени также с рациональными коэффициентами.
Лит.: Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.
| "БСЭ" >> "Н" >> "НЕ" >> "НЕП" |
Статья про "Неприводимый многочлен" в Большой Советской Энциклопедии была прочитана 739 раз
| Коптим скумбрию в коробке |
| Чистим кильку легко и просто |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная