Ньютона метод

Значение слова "Ньютона метод" в Большой Советской Энциклопедии

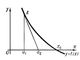Ньютона метод, метод приближённого нахождения корня x₀ уравнения f (x) = 0, называемый также методом касательных. Ньютона метод состоит в том, что по исходному («первому») приближению х = a₁ находят второе (более точное), проводя касательную к графику (см. рис.) у = f (x) в точке А [а₁ f (a₁)] до её пересечения с осью Ox; точка пересечения х = a₁- f (a₁)/f’(a₁) и принимается за новое значение a₂. корня. Повторяя в случае необходимости этот процесс, получают всё более и более точные приближения a₂, a₃,... корня x₀ при условии, что производная f’(x) монотонна и сохраняет знак на сегменте, содержащем x₀. Ошибка e₂ = x₀-a₂ нового значения a₂ связана со старой ошибкой e₁ = x₀- a₁ формулой

, где

- значение второй производной функции f (x) в некоторой точке x, лежащей между x₀ и a₁. Иногда рекомендуется Ньютона метод применять одновременно с к.-л. другим способом, например с линейного интерполирования методом. Ньютона метод допускает обобщения, которые позволяют применять его для решения уравнений F (x) = 0 в нормированных пространствах (F- оператор в этом пространстве), в частности для решения систем уравнений и функциональных уравнений. Метод разработан И. Ньютоном в 1669.

Рис. к ст. Ньютона метод.

В Большой Советской Энциклопедии рядом со словом "Ньютона метод"

Ньютона кольца | Буква "Н" | В начало | Буквосочетание "НЫ" | Ньютона механика

Статья про слово "Ньютона метод" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

Florists in america

business support in USA