Библиотека DJVU
БСЭ
Статистика:
Периодические решения
Значение слова "Периодические решения" в Большой Советской Энциклопедии
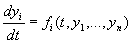, i = 1,..., n (1)Это такие решения yi = ji (t), которые состоят из периодических одного и того же периода функций независимого переменного t, то есть для всех значений t
ji (t + t) = ji (t)
где t > 0—период решения. Если система (1) стационарна, то есть функции fi = Fi (yi,.... yn), где i = 1,..., n, явным образом не зависят от t, то в фазовом пространстве (yi,..., yi) Периодические решения отвечают замкнутые траектории. В частном случае эти траектории могут вырождаться в точки покоя
, где 
, которым соответствуют тривиальные (постоянные) Периодические решения Что касается нетривиальных Периодические решения, то задача о нахождении их решена лишь для дифференциальных уравнений специальных типов.В теории нелинейных колебаний особое значение имеет система двух уравнений
, 
(2)фазовым пространством которой является плоскость (х, у). Точки покоя системы (2) находятся из системы уравнений: Р (х, у) = 0, Q (x, у) = 0. Система (2) заведомо не допускает нетривиальных Периодические решения, если
(критерий Бендиксона). Обычным приёмом обнаружения нетривиальных Периодические решения системы (2) (если они существуют) является построение такой ограниченной кольцеобразной области K (см. рис.), что все траектории входят в неё при t ® +¥ или при t ® -¥; если область К не содержит точек покоя системы (2), то в К обязательно найдётся замкнутая траектория, которой соответствует нетривиальное Периодические решения (принцип Пуанкаре — Бендиксона). Другой подход к обнаружению Периодические решения даёт изучение поведения решений в окрестностях особых точек; именно, в окрестности центра интегральные кривые системы (2) замкнуты и им соответствуют нетривиальные Периодические решенияЛит.: Немыцкий В. В. и Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.— Л., 1949; Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959; Стокер Дж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953.
Рис. к ст. Периодические решения.
В Большой Советской Энциклопедии рядом со словом "Периодические решения"
Периодические психозы | Буква "П" | В начало | Буквосочетание "ПЕ" | Периодический закон МенделееваСтатья про слово "Периодические решения" в Большой Советской Энциклопедии была прочитана 0 раз
Интересное