БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ
Навигация:
Библиотека DJVU
Photogallery
БСЭ
 Статистика:

Плотность вероятности

Значение слова "Плотность вероятности" в Большой Советской Энциклопедии


Плотность вероятности случайной величины X, функция р(х), такая, что при любых a и b вероятность неравенства а < Х < b равна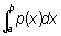

.

  Например, если Х имеет нормальное распределение, то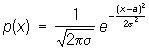

.

  Если Плотность вероятности p(x) непрерывна, то при достаточно малых dx вероятность неравенства x < X < x + dx приближённо равна p(x)dx. Плотность вероятности всегда удовлетворяет условиям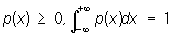

.

  Аналогично определяют Плотность вероятности p(x1,...,xs) для нескольких случайных величин X1, X2, ..., Xs (т. н. совместную Плотность вероятности): при любых ai, bi вероятность одновременного выполнения неравенств a1 < Xi < b1, . . ., as < Xs < bs равна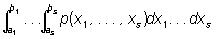

.

  Если существует совместная Плотность вероятности X1, Х2, ..., Xs, то для независимости этих величин необходимо и достаточно. чтобы совместная Плотность вероятности была произведением Плотность вероятности отдельных величин Xi, i = 1, 2, . . ., s.

 

 

В Большой Советской Энциклопедии рядом со словом "Плотность вероятности"

Плотность | Буква "П" | В начало | Буквосочетание "ПЛ" | Плотность населения


Статья про слово "Плотность вероятности" в Большой Советской Энциклопедии была прочитана 9574 раз

Интересное