


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Проекция (в геометрии)
Определение "Проекция (в геометрии)" в Большой Советской Энциклопедии
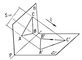 |
| Проекция. Рис. |
 |
| Проекция. Рис. |
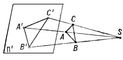
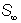 (см. рис. 3). При этом все проектирующие прямые параллельны и Проекция (в геометрии) называется параллельной или цилиндрической. Взаимно однозначное соответствие между точками плоскостей П и П", установленное при помощи параллельного проектирования, называется перспективно-аффинным или родственным (см. Аффинные преобразования).
(см. рис. 3). При этом все проектирующие прямые параллельны и Проекция (в геометрии) называется параллельной или цилиндрической. Взаимно однозначное соответствие между точками плоскостей П и П", установленное при помощи параллельного проектирования, называется перспективно-аффинным или родственным (см. Аффинные преобразования).
 |
| Проекция. Рис. |
Центральные и параллельные (в частности, ортогональные) Проекция (в геометрии) широко используют в начертательной геометрии, причём получаются различные виды изображений (перспективные, аксонометрические и др.). Специальные виды проектирования на плоскость, сферу и др. поверхности применяются в географии, астрономии, кристаллографии, топографии и т.д. Таковы картографические проекции, гномонические проекции, стереографические проекции и др. Об ортогональной проекции направленных отрезков (векторов) см. в ст. Векторное исчисление.
Н. Ф. Четверухин.
| "БСЭ" >> "П" >> "ПР" >> "ПРО" >> "ПРОЕ" |
Статья про "Проекция (в геометрии)" в Большой Советской Энциклопедии была прочитана 796 раз
| Коптим скумбрию в коробке |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Объединённая партия гаитянских коммунистов
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная