


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Пуассона уравнение
Определение "Пуассона уравнение" в Большой Советской Энциклопедии
Пуассона уравнение, уравнение с частными производными вида Du = f, где D —оператор Лапласа: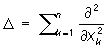
При n = 3 этому уравнению удовлетворяет потенциал u (х, у, z) объёмных масс, распределённых с плотностью f (x, у, z)/4p (в областях, где f = 0 потенциал u удовлетворяет уравнению Лапласа), а также потенциал объёмно распределённых электрических зарядов. При этом плотность распределения f должна удовлетворять известным требованиям гладкости (например, условию непрерывности частных производных). Если функция f отлична от нуля лишь в конечной области G, ограничена и имеет непрерывные частные производные первого порядка, то при n = 2 частное решение Пуассона уравнение имеет вид: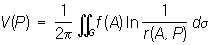
а при n = 3: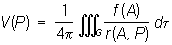
где r (А, Р) — расстояние между переменной точкой интегрирования А и некоторой точкой Р. В более подробной записи
V (х, у, z) = 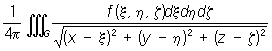
Решение краевых задач для Пуассона уравнение сводится подстановкой 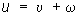 к решению краевых задач для уравнения Лапласа Dw = 0.
к решению краевых задач для уравнения Лапласа Dw = 0.
Пуассона уравнение впервые (1812) было изучено С. Д. Пуассоном.
| "БСЭ" >> "П" >> "ПУ" >> "ПУА" |
Статья про "Пуассона уравнение" в Большой Советской Энциклопедии была прочитана 855 раз
| Английское куриное карри |
| Английское куриное карри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная