


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Потенциал (математич., физич.)
Определение "Потенциал (математич., физич.)" в Большой Советской Энциклопедии
Потенциал, потенциальная функция, понятие, характеризующее широкий класс физических силовых полей (электрическое, гравитационное и т.п.) и вообще поля физических величин, представляемых векторами (поле скоростей в жидкости и т.п.). В электростатическое поле Потенциал (математич., физич.) вводится как вспомогательная функция, пространственные производные которой - компоненты напряжённости электрического поля в данной точке; в гидродинамике - компоненты скорости в данной точке и т.п. При этом Потенциал (математич., физич.) в ряде случаев имеет и др. важный физический смысл. Так, в электростатическом поле он численно равен энергии, необходимой для удаления единичного положительного заряда из данной точки в бесконечность (с обратным знаком).
В общем случае Потенциал (математич., физич.) векторного поля а (х, у, z) - скалярная функция u (х, у, z), такая, что а = grad u, т. е. 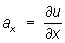 ,
, 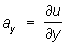 ,
, 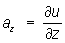 , где ax, ay, az; - компоненты поля a в системе декартовых координат Oxyz. Если такую функцию можно ввести, то векторное поле а называют потенциальным. Иногда Потенциал (математич., физич.) называют функцию U = -u (например, в электростатике). Потенциал (математич., физич.) векторного поля а определяется не однозначно, а с точностью до постоянного слагаемого. Поэтому при изучении потенциального поля представляют интерес лишь разности Потенциал (математич., физич.) в различных точках поля. Уравнение u (х, у, z) = с геометрически представляет поверхность, во всех точках которой Потенциал (математич., физич.) имеет одинаковую величину; такие поверхности называют поверхностями уровня, или эквипотенциальными поверхностями.
, где ax, ay, az; - компоненты поля a в системе декартовых координат Oxyz. Если такую функцию можно ввести, то векторное поле а называют потенциальным. Иногда Потенциал (математич., физич.) называют функцию U = -u (например, в электростатике). Потенциал (математич., физич.) векторного поля а определяется не однозначно, а с точностью до постоянного слагаемого. Поэтому при изучении потенциального поля представляют интерес лишь разности Потенциал (математич., физич.) в различных точках поля. Уравнение u (х, у, z) = с геометрически представляет поверхность, во всех точках которой Потенциал (математич., физич.) имеет одинаковую величину; такие поверхности называют поверхностями уровня, или эквипотенциальными поверхностями.
Для поля тяготения, образованного помещенной в точку A (x, h, x) точечной массой m, Потенциал (математич., физич.) (ньютонов Потенциал (математич., физич.)) имеет в точке Р (х, у, z) вид:
u (х, у, z) = Gm/r, (1)
где 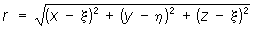 , G - постоянная тяготения. При наложении полей их Потенциал (математич., физич.) алгебраически складываются. Если поле тяготения обусловлено некоторой массой плотности r(x, h, x), занимающей объём Т, то его можно рассматривать как результат наложения элементарных полей, образованных бесконечно малыми телами массы rdxdhdx. Ньютонов Потенциал (математич., физич.) такого поля представляется интегралом
, G - постоянная тяготения. При наложении полей их Потенциал (математич., физич.) алгебраически складываются. Если поле тяготения обусловлено некоторой массой плотности r(x, h, x), занимающей объём Т, то его можно рассматривать как результат наложения элементарных полей, образованных бесконечно малыми телами массы rdxdhdx. Ньютонов Потенциал (математич., физич.) такого поля представляется интегралом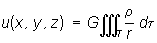 . (2)
. (2)
Потенциал (математич., физич.) u (х, у, z) - непрерывная функция во всём пространстве вместе со своими частными производными 1-го порядка; вне тела объёма Т функция u (х, у, z) удовлетворяет Лапласа уравнению, внутри - Пуассона уравнению.
Если притягивающие массы распределены с плотностью rпов по поверхности S (простой слой), то Потенциал (математич., физич.) образованного ими поля выражается интегралом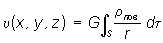 . (3)
. (3)
Потенциал (математич., физич.) простого слоя u(x, у, z) - непрерывная во всём пространстве функция; при пересечении поверхности S нормальная производная функции w(х, у, z) испытывает разрыв, равный 4pG/rпов. Неограниченно сближая две поверхности, на которых расположены простые слои с плотностями rпов и -rпов, и одновременно увеличивая rпов до бесконечности, но так, чтобы был конечным предел 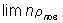 = m, где n - нормальное расстояние между поверхностями, приходят к понятию Потенциал (математич., физич.) двойного слоя:
= m, где n - нормальное расстояние между поверхностями, приходят к понятию Потенциал (математич., физич.) двойного слоя: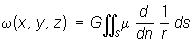 (4)
(4)
Потенциал (математич., физич.) двойного слоя w(х, у, z) - непрерывная функция во всём пространстве вне S; при пересечении поверхности S функция w(х, у, z) испытывает разрыв, равный 4pGm. Функции u(х, у, z) и w(х, у, z) удовлетворяют уравнению Лапласа.
Если тело объёма Т - бесконечный цилиндр с поперечным сечением D и плотность r вещества цилиндра постоянна вдоль каждой прямой, параллельной образующим цилиндра, то формула (2) приводит к понятию логарифмического потенциала:
u (х, у) = 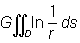 . (5)
. (5)
В виде суммы Потенциал (математич., физич.) простого и двойного слоев может быть представлена любая гармоническая функция; этим объясняется важность теории Потенциал (математич., физич.)
Лит.: Гюнтер Н. М., Теория потенциала и её применение к основным задачам математической физики, М., 1953; Сретенский Л. Н., Теория ньютоновского потенциала, М. - Л., 1946; Тамм И. Е., Основы теории электричества, 7 изд., М., 1957; Идельсон Н. И., Теория потенциала с приложениями к теории фигуры Земли и геофизике, 2 изд., Л. - М., 1936.
В. И. Битюцков.
| "БСЭ" >> "П" >> "ПО" >> "ПОТ" >> "ПОТЕ" |
Статья про "Потенциал (математич., физич.)" в Большой Советской Энциклопедии была прочитана 928 раз
| Пицца в сковороде |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная