


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Равномерная непрерывность
Определение "Равномерная непрерывность" в Большой Советской Энциклопедии
Равномерная непрерывность, важное понятие математического анализа. Функция f (x) называется равномерно-непрерывной на данном множестве, если для всякого e > 0 можно найти такое d = d(e) > 0, что êf (x1) — f (x2)ê<e для любой пары чисел x1 и x2 из данного множества, удовлетворяющей условию ïx1—x2ï< d (ср. Непрерывная функция). Например, функция f (x) = x2 равномерно непрерывна на отрезке [0, 1]: если 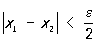 , то
, то  (так как для 0 £ x1 £ 1, 0 £ x2 £ 1 обязательно ïx1 + x2ï£ 2). Вообще функция, непрерывная в каждой точке отрезка [а, b], равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места.
(так как для 0 £ x1 £ 1, 0 £ x2 £ 1 обязательно ïx1 + x2ï£ 2). Вообще функция, непрерывная в каждой точке отрезка [а, b], равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места.
Так, например, функция  непрерывна в каждой точке интервала 0 < x < 1, но не является равномерно непрерывной в этом интервале, потому что, например, при e = 1 для любого d > 0 (d < 1) мы имеем удовлетворяющие неравенству ïx1 — x2ï < d числа x1 =
непрерывна в каждой точке интервала 0 < x < 1, но не является равномерно непрерывной в этом интервале, потому что, например, при e = 1 для любого d > 0 (d < 1) мы имеем удовлетворяющие неравенству ïx1 — x2ï < d числа x1 =  и x2 = d , для которых
и x2 = d , для которых  .
.
| "БСЭ" >> "Р" >> "РА" >> "РАВ" |
Статья про "Равномерная непрерывность" в Большой Советской Энциклопедии была прочитана 637 раз
| Коптим скумбрию в коробке |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная