


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Равносильные уравнения
Определение "Равносильные уравнения" в Большой Советской Энциклопедии
Равносильные уравнения, уравнения, имеющие одно и то же множество корней (в случае кратных корней нужно, чтобы кратности соответствующих корней совпадали). Так, из трёх уравнений: 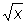 = 2, 3х — 7 = 5, (х — 4)2 = 0, первое и второе — Равносильные уравнения, а первое и третье не Равносильные уравнения (т.к. кратность корня х = 4 для первого уравнения равна 1, а для третьего равна 2). Если к обеим частям уравнения прибавить один и тот же многочлен от х или умножить обе части на одно и то же число, не равное 0, то получим уравнение, равносильное данному. Например, x2 — x + 1 = x — 1 и x2 — 2x + 2 = 0 — Равносильные уравнения (к обеим частям первого прибавлен многочлен: — х + 1); 0,01х2 — 0,37х + 1 = 0 и x2 — 37x + 100 = 0 — также Равносильные уравнения (обе части первого умножены на 100). Но если умножить или разделить обе части уравнения на многочлен степени не ниже 1, то полученное уравнение, вообще говоря, не будет равносильным данному. Например, х — 1 = 0 и (х — 1)(х + 1) = 0 — не Равносильные уравнения (корень х = — 1 второго не является корнем первого). Понятие «Равносильные уравнения» приобретает точный смысл, когда указано поле, в котором лежат корни уравнений. Например, x2 — 1 = 0 и x4 — 1 = 0 — Равносильные уравнения в поле действительных чисел (множество корней как для одного, так и для другого состоит из 2 чисел: x1 = 1, x2 = —1). Но они не Равносильные уравнения в поле комплексных чисел, т.к. второе имеет ещё 2 мнимых корня: x3 = i, x2 = — i. Понятие Равносильные уравнения можно применять и к системе уравнений. Например, если Р (х, у) и Q (x, у) — два многочлена от переменных х и у и а, b, с и d — числа (действительные или комплексные), то две системы: Р (х, у) = 0, Q (x, у) = 0 и aP (x, у) + bQ (x, y) = 0, cP (x, y) + dQ (x, y) = 0 равносильны тогда, когда определитель ad — bc ¹ 0.
= 2, 3х — 7 = 5, (х — 4)2 = 0, первое и второе — Равносильные уравнения, а первое и третье не Равносильные уравнения (т.к. кратность корня х = 4 для первого уравнения равна 1, а для третьего равна 2). Если к обеим частям уравнения прибавить один и тот же многочлен от х или умножить обе части на одно и то же число, не равное 0, то получим уравнение, равносильное данному. Например, x2 — x + 1 = x — 1 и x2 — 2x + 2 = 0 — Равносильные уравнения (к обеим частям первого прибавлен многочлен: — х + 1); 0,01х2 — 0,37х + 1 = 0 и x2 — 37x + 100 = 0 — также Равносильные уравнения (обе части первого умножены на 100). Но если умножить или разделить обе части уравнения на многочлен степени не ниже 1, то полученное уравнение, вообще говоря, не будет равносильным данному. Например, х — 1 = 0 и (х — 1)(х + 1) = 0 — не Равносильные уравнения (корень х = — 1 второго не является корнем первого). Понятие «Равносильные уравнения» приобретает точный смысл, когда указано поле, в котором лежат корни уравнений. Например, x2 — 1 = 0 и x4 — 1 = 0 — Равносильные уравнения в поле действительных чисел (множество корней как для одного, так и для другого состоит из 2 чисел: x1 = 1, x2 = —1). Но они не Равносильные уравнения в поле комплексных чисел, т.к. второе имеет ещё 2 мнимых корня: x3 = i, x2 = — i. Понятие Равносильные уравнения можно применять и к системе уравнений. Например, если Р (х, у) и Q (x, у) — два многочлена от переменных х и у и а, b, с и d — числа (действительные или комплексные), то две системы: Р (х, у) = 0, Q (x, у) = 0 и aP (x, у) + bQ (x, y) = 0, cP (x, y) + dQ (x, y) = 0 равносильны тогда, когда определитель ad — bc ¹ 0.
А. И. Маркушевич.
| "БСЭ" >> "Р" >> "РА" >> "РАВ" |
Статья про "Равносильные уравнения" в Большой Советской Энциклопедии была прочитана 699 раз
| Ананасы на гриле |
| Ананасы на гриле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная