


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Регрессия (математич.)
Определение "Регрессия (математич.)" в Большой Советской Энциклопедии
Регрессия в теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости у = f(х), когда каждому значению независимой переменной х соответствует одно определённое значение величины у, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины у. Если при каждом значении х = xi наблюдается ni, значений yi1, ..., 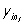 величины у, то зависимость средних арифметических
величины у, то зависимость средних арифметических 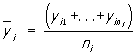 от xi и является Регрессия (математич.) в статистическом понимании этого термина. Примером такого рода зависимости служит, в частности, зависимость средних диаметров сосен от их высот; см. табл. в ст. Корреляция.
от xi и является Регрессия (математич.) в статистическом понимании этого термина. Примером такого рода зависимости служит, в частности, зависимость средних диаметров сосен от их высот; см. табл. в ст. Корреляция.
Изучение Регрессия (математич.) в теории вероятностей основано на том, что случайные величины Х и Y, имеющие совместное распределение вероятностей, связаны вероятностной зависимостью: при каждом фиксированном значении Х = х величина Y является случайной величиной с определённым (зависящим от значения х) условным распределением вероятностей. Регрессия (математич.) величины Y по величине Х определяется условным математическим ожиданием Y, вычисленным при условии, что Х = х:
Е(Y êх) = u(х).
Уравнение у = u(х), в котором х играет роль «независимой» переменной, называется уравнением регрессии, а соответствующий график — линией регрессии величины Y по X. Точность, с которой уравнение Регрессия (математич.) Y по Х отражает изменение Y в среднем при изменении х, измеряется условной дисперсией величины Y, вычисленной для каждого значения Х = х:
D(Y êх) = s2(x).
Если s2(х) = 0 при всех значениях х, то можно с достоверностью утверждать, что Y и Х связаны строгой функциональной зависимостью Y = u(X). Если s2(х) = 0 при всех значениях х и u(х) не зависит от х, то говорят, что Регрессия (математич.) Y по Х отсутствует. Аналогичным образом определяется Регрессия (математич.) Х по Y и в частности, уравнение Регрессия (математич.) х = u(у), = Е(ХïY = у). Функции у = u(х) и х = u(у), вообще говоря, не являются взаимно обратными.
Линии Регрессия (математич.) обладают следующим замечательным свойством: среди всех действительных функций f (х) минимум математического ожидания Е[Y — f(X)]2 достигается для функции f(x) = u(х), т. е. Регрессия (математич.) Y по Х даёт наилучшее, в указанном смысле, представление величины Y по величине X. Это свойство используется для прогноза Y по X: если значение Y непосредственно не наблюдается и эксперимент позволяет регистрировать лишь компоненту Х вектора (X, Y), то в качестве прогнозируемого значения Y используют величину u (X).
Наиболее простым является случай, когда Регрессия (математич.) Y по Х линейна:
Е(Yïx) = b0 + b1x.
Коэффициенты b0 и b1, называются коэффициентами регрессии, определяются равенствами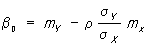 ,
, 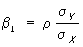
где mХ и mY — математические ожидания Х и Y, 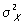 и
и 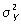 — дисперсии Х и Y, а r — коэффициент корреляции между Х и Y. Уравнение Регрессия (математич.) при этом выражается формулой
— дисперсии Х и Y, а r — коэффициент корреляции между Х и Y. Уравнение Регрессия (математич.) при этом выражается формулой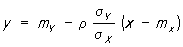
В случае, когда совместное распределение Х и Y нормально, обе линии Регрессия (математич.) у = u(х) и х = u(у) являются прямыми.
Если Регрессия (математич.) Y по Х отлична от линейной, то последнее уравнение есть линейная аппроксимация истинного уравнения Регрессия (математич.): математическое ожидание Е[Y — b0 — b1X]2 достигает минимума b0 и b1 при b0 = b0 и b1 = b1. Особенно часто встречается случай уравнения Регрессия (математич.), выражающегося линейной комбинацией тех или иных заданных функций:
у = u(Х) = b0j0(x) + b1j1(x) + ... + bmjm(x).
Наиболее важное значение имеет параболическая (полиномиальная) Регрессия (математич.), при которой j0(x) = 1 , j1(x) = x, ..., jm(x) = xm.
Понятие Регрессия (математич.) применимо не только к случайным величинам, но и к случайным векторам. В частности, если Y — случайная величина, а Х = (X1, ..., Xk) — случайный вектор, имеющие совместное распределение вероятностей, то Регрессия (математич.) Y по X определяется уравнением
y = u ( x1, ..., xk),
где u( x1, ..., xk) = E{YïX = x1, ... , Xk = xk}.
Если
u ( x1, ..., xk) = b0 + b1x1 + ... + bkxk,
то Регрессия (математич.) называется линейной. Эта форма уравнения Регрессия (математич.) включает в себя многие типы Регрессия (математич.) с одной независимой переменной, в частности полиномиальная Регрессия (математич.) Y по Х порядка k сводится к линейной Регрессия (математич.) Y по X1, ..., Xk, если положить Xk = Xk.
Простым примером Регрессия (математич.) Y по Х является зависимость между Y и X, которая выражается соотношением: Y = u(X) + d, где u(x) = Е(Y IX = х), а случайные величины Х и d независимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи у = u(х) между неслучайными величинами у и х.
На практике обычно коэффициенты Регрессия (математич.) в уравнении у = u(х) неизвестны и их оценивают по экспериментальным данным (см. Регрессионный анализ).
Первоначально термин «Регрессия (математич.)» был употреблен английским статистиком Ф. Гальтоном (1886) в теории наследственности в следующем специальном смысле: «возвратом к среднему состоянию» (regression to mediocrity) было названо явление, состоящее в том, что дети тех родителей, рост которых превышает среднее значение на а единиц, имеют в среднем рост, превышающий среднее значение меньше чем на а единиц.
Лит.: Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Кендалл М. Дж., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973.
А. В. Прохоров.
| "БСЭ" >> "Р" >> "РЕ" >> "РЕГ" |
Статья про "Регрессия (математич.)" в Большой Советской Энциклопедии была прочитана 932 раз
| Буддийская молитва в Камбодже |
| Буддийская молитва в Камбодже |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная