


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Регрессионный анализ
Определение "Регрессионный анализ" в Большой Советской Энциклопедии
Регрессионный анализ, раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным (см. Регрессия). Цель Регрессионный анализ состоит в определении общего вида уравнения регрессии, построении оценок неизвестных параметров, входящих в уравнение регрессии, и проверке статистических гипотез о регрессии. При изучении связи между двумя величинами по результатам наблюдений (x1, y1), ..., (xn, yn) в соответствии с теорией регрессии предполагается, что одна из них Y имеет некоторое распределение вероятностей при фиксированном значении х другой, так что
Е(Y ï х) = g(x, b) и D(Y ï х) = s2h2(x),
где b обозначает совокупность неизвестных параметров, определяющих функцию g(х), a h(x) есть известная функция х (в частности, тождественно равная 1). Выбор модели регрессии определяется предположениями о форме зависимости g(х, b) от х и b. Наиболее естественной с точки зрения единого метода оценки неизвестных параметров b является модель регрессии, линейная относительно b:
g(x, b) = b0g0(x) + ... + bkgk(x).
Относительно значений переменной х возможны различные предположения в зависимости от характера наблюдений и целей анализа. Для установления связи между величинами в эксперименте используется модель, основанная на упрощённых, но правдоподобных допущениях: величина х является контролируемой величиной, значения которой заранее задаются при планировании эксперимента, а наблюдаемые значения у представимы в виде
yi = g(xi, b) + ei, i = 1, ..., k,
где величины ei характеризуют ошибки, независимые при различных измерениях и одинаково распределённые с нулевым средним и постоянной дисперсией s2. Случай неконтролируемой переменной х отличается тем, что результаты наблюдений (xi, yi), ..., (xn, yn) представляют собой выборку из некоторой двумерной совокупности. И в том, и в другом случае Регрессионный анализ производится одним и тем же способом, однако интерпретация результатов существенно различается (если обе исследуемые величины случайны, то связь между ними изучается методами корреляционного анализа).
Предварительное представление о форме графика зависимости g(x) от х можно получить по расположению на диаграмме рассеяния (называемой также корреляционным полем, если обе переменные случайные) точек (xi, 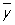 (xi)), где
(xi)), где 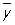 (xi) — средние арифметические тех значений у, которые соответствуют фиксированному значению xi. Например, если расположение этих точек близко к прямолинейному, то допустимо использовать в качестве приближения линейную регрессию. Стандартный метод оценки линии регрессии основан на использовании полиномиальной модели (m ³ 1)
(xi) — средние арифметические тех значений у, которые соответствуют фиксированному значению xi. Например, если расположение этих точек близко к прямолинейному, то допустимо использовать в качестве приближения линейную регрессию. Стандартный метод оценки линии регрессии основан на использовании полиномиальной модели (m ³ 1)
y(x, b) = b0 + b1x + ... + bmxm
(этот выбор отчасти объясняется тем, что всякую непрерывную на некотором отрезке функцию можно приблизить полиномом с любой наперёд заданной степенью точности). Оценка неизвестных коэффициентов регрессии b0, ..., bm и неизвестной дисперсии s2 осуществляется наименьших квадратов методом. Оценки 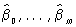 параметров b0, ..., bm, полученные этим методом, называются выборочными коэффициентами регрессии, а уравнение
параметров b0, ..., bm, полученные этим методом, называются выборочными коэффициентами регрессии, а уравнение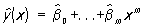
определяет т. н. эмпирическую линию регрессии. Этот метод в предположении нормальной распределённости результатов наблюдений приводит к оценкам для b0, ..., bm и s2, совпадающим с оценками наибольшего правдоподобия (см. Максимального правдоподобия метод). Оценки, полученные этим методом, оказываются в некотором смысле наилучшими и в случае отклонения от нормальности. Так, если проверяется гипотеза о линейной регрессии, то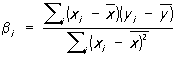 ,
, 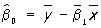 ,
,
где 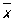 и
и  — средние арифметические значений xi и yi, и оценка
— средние арифметические значений xi и yi, и оценка 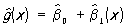 будет несмещенной для g(х), а её дисперсия будет меньше, чем дисперсия любой другой линейной оценки. При допущении, что величины yi нормально распределены, наиболее эффективно осуществляется проверка точности построенной эмпирической регрессионной зависимости и проверка гипотез о параметрах регрессионной модели. В этом случае построение доверительных интервалов для истинных коэффициентов регрессии b0, ..., bm и проверка гипотезы об отсутствии регрессионной связи bi = 0, i = 1, ..., m) производится с помощью Стьюдента распределения.
будет несмещенной для g(х), а её дисперсия будет меньше, чем дисперсия любой другой линейной оценки. При допущении, что величины yi нормально распределены, наиболее эффективно осуществляется проверка точности построенной эмпирической регрессионной зависимости и проверка гипотез о параметрах регрессионной модели. В этом случае построение доверительных интервалов для истинных коэффициентов регрессии b0, ..., bm и проверка гипотезы об отсутствии регрессионной связи bi = 0, i = 1, ..., m) производится с помощью Стьюдента распределения.
В более общей ситуации результаты наблюдений y1, ..., yn рассматриваются как независимые случайные величины с одинаковыми дисперсиями и математическими ожиданиями
Eyi, = b1 x1i + ... + bkxki, i = 1, ..., n,
где значения xji, j = 1, ..., k предполагаются известными. Эта форма линейной модели регрессии является общей в том смысле, что к ней сводятся модели более высоких порядков по переменным x1, ..., xk. Кроме того, некоторые нелинейные относительно параметров bi; модели подходящим преобразованием также сводятся к указанной линейной форме.
Регрессионный анализ является одним из наиболее распространённых методов обработки результатов наблюдений при изучении зависимостей в физике, биологии, экономике, технике и др. областях. На модели Регрессионный анализ основаны такие разделы математической статистики, как дисперсионный анализ и планирование эксперимента; модели Регрессионный анализ широко используются в статистическом анализе многомерном.
Лит.: Юл Дж. Э., Кендэл М. Дж., Теория статистики, пер. с англ., 14 изд., М., 1960; Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; Айвазян С. А., Статистическое исследование зависимостей, М., 1968; Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968. См. также лит. при ст. Регрессия.
А. В. Прохоров.
| "БСЭ" >> "Р" >> "РЕ" >> "РЕГ" |
Статья про "Регрессионный анализ" в Большой Советской Энциклопедии была прочитана 760 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная