Библиотека DJVU
БСЭ
Статистика:
Результант
Значение слова "Результант" в Большой Советской Энциклопедии
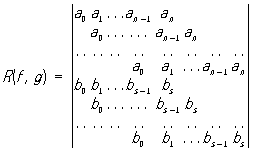,где на свободных местах стоят нули; коэффициенты a0, a1, ..., an занимают s строк, а коэффициенты b0 b1 , ..., bn занимают n строк. Если a0 ¹ 0 и b0 ¹ 0, то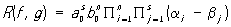
,где a1, a2, ..., an - корни f(x), b1, b2,. .., bs - корни g(x). Результант равен нулю тогда и только тогда, когда f(x) и g(х) обладают общим корнем или когда их старшие коэффициенты оба равны нулю.
Пусть даны 2 уравнения Р(х, у) = 0 и Q(x, y) = 0, где Р и Q - многочлены относительно х и у. Если расположить эти многочлены по степеням х и приравнять нулю Результант получающихся многочленов, то получится уравнение относительно у степени, не превосходящей sn, где n - степень Р относительно х и у, a s - степень Q. Если x = x0, у = y0 - решение данной системы уравнений, то у = y0 является корнем уравнения R(f, g) = 0. Это позволяет свести решение системы двух уравнений к решению одного уравнения.
Результант многочлена и его производной с точностью до знака равен дискриминанту многочлена. Равенство нулю дискриминанта показывает наличие у многочлена кратных корней.
Лит.: Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971.
В Большой Советской Энциклопедии рядом со словом "Результант"
Резорцин | Буква "Р" | В начало | Буквосочетание "РЕ" | РезусСтатья про слово "Результант" в Большой Советской Энциклопедии была прочитана 0 раз
Интересное