


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Сжатых отображений принцип
Определение "Сжатых отображений принцип" в Большой Советской Энциклопедии
Сжатых отображений принцип, одно из основных положений теории метрических пространств о существовании и единственности неподвижной точки множества при некотором специальном («сжимающем») отображении его в себя. Сжатых отображений принцип применяют главным образом в теории дифференциальных и интегральных уравнений.
Произвольное отображение А метрического пространства М в себя, которое каждой точке х из М сопоставляет некоторую точку у = Ax из М, порождает в пространстве М уравнение
Ax = х. (*)
Действие отображения А на точку х можно интерпретировать как перемещение её в точку у = Ax. Точка х называется неподвижной точкой отображения А, если выполняется равенство (*). Т. о. вопрос о разрешимости уравнения (*) является вопросом о нахождении неподвижных точек отображения А.
Отображение А метрического пространства М в себя называется сжатым, если существует такое положительное число a < 1, что для любых точек х и у из М выполняется неравенство
d (Ax, Ау) £ ad (х, у),
где символ d (u, u) означает расстояние между точками u и u метрического пространства М.
Сжатых отображений принцип утверждает, что каждое сжатое отображение полного метрического пространства в себя имеет, и притом только одну, неподвижную точку. Кроме того, для любой начальной точки x0 из М последовательность {xn}, определяемая рекуррентными соотношениями
xn = Axn-1, n = 1,2,...,
имеет своим пределом неподвижную точку х отображения А. При этом справедлива следующая оценка погрешности: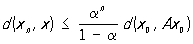 .
.
Сжатых отображений принцип позволяет единым методом доказывать важные теоремы о существовании и единственности решений дифференциальных, интегральных и др. уравнений. В условиях применимости Сжатых отображений принцип решение может быть с наперёд заданной точностью вычислено последовательных приближений методом.
С помощью определённого выбора полного метрического пространства М и построения отображения А эти задачи сводят предварительно к уравнению (*), а затем находят условия, при которых отображение А оказывается сжатым.
Лит.: Смирнов В. И., Курс высшей математики, т. 5, М., 1959.
Ш. А. Алимов.
| "БСЭ" >> "С" >> "СЖ" |
Статья про "Сжатых отображений принцип" в Большой Советской Энциклопедии была прочитана 851 раз
| Бургер двойного помола |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная