


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Средние
Определение "Средние" в Большой Советской Энциклопедии
Средние, средние значения, числовая характеристика группы чисел или функций.
1) Средним для данной группы чисел x1, x2,..... xn называется любое число, заключённое между наименьшим и наибольшим из них. Наиболее употребительными Средние являются: арифметическое среднее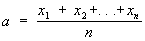 ,
,
геометрическое среднее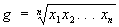 ,
,
гармоническое среднее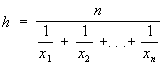 ,
,
квадратичное среднее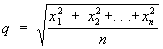 .
.
Если все числа xi (i = l,2,..., n) положительны, то можно для любого a ¹ 0 определить степенное Средние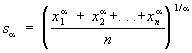
частными случаями которого являются арифметическое, гармоническое и квадратичное Средние, именно: s (а равняется a, h и q соответственно при a = 1, —1 и 2. При a ® 0 степенное С, sa стремится к геометрическому Средние, так что можно считать s0 = g. Важную роль играет неравенство sa £ sb, если a £ b, в частности
h £ g £ a £ q.
Арифметическое и квадратичное Средние находят многочисленные применения в теории вероятностей, математической статистике, при вычислении по методу наименьших квадратов и др. Указанные выше Средние могут быть получены из формулы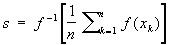 ,
,
где f-1(h) — функция, обратная к f (x) (см. Обратная функция), при соответствующем подборе функции f (x). Так, арифметическое Средние получается, если f(x) = x, геометрическое Средние — если f (x) = log x, гармоническое Средние — если f (x) = 1/x, квадратичное Средние — если f (x) = x2.
Наряду со степенными Средние рассматривают взвешенные степенные Средние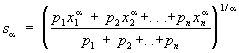
в частности при a = 1,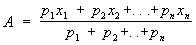 ,
,
которые переходят в обыкновенные степенные Средние при р1 = р2 =... = pn. Взвешенные Средние особенно важны при математической обработке результатов наблюдений (см. Наблюдений обработка), когда различные наблюдения производятся с разной точностью (с разным весом).
2) Арифметико-геометрическое среднее. Для пары положительных чисел а и b составляются арифметическое Средние a1 и геометрическое Средние g1. Затем для пары a1, g1 снова находятся арифметическое Средние a2 и геометрическое Средние g2 и т.д. Общий предел последовательностей an и gb, существование которого было доказано К. Гауссом, называется арифметико-геометрическим Средние чисел а и b; он важен в теории эллиптических функций.
3) Средним значением функции называется любое число, заключённое между наименьшим и наибольшим её значениями. В дифференциальном и интегральном исчислении имеется ряд «теорем о среднем», устанавливающих существование таких точек, в которых функция или её производная получает то или иное среднее значение. Наиболее важной теоремой о Средние в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если f (x) непрерывна на отрезке [а, b] и дифференцируема в интервале (а, b), то существует точка с, принадлежащая интервалу (а, b), такая, что f (b) — f (a) = (b—a) f’(c). В интегральном исчислении наиболее важной теоремой о Средние является следующая: если f (x) непрерывна на отрезке [а, b], а j(x) сохраняет постоянный знак, то существует точка с из интервала (а, b) такая, что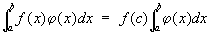 .
.
В частности, если j(x) = 1, то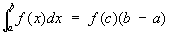 .
.
Вследствие этого под средним значением функции f (x) на отрезке [а, b] обычно понимают величину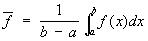 .
.
Аналогично определяют среднее значение функции нескольких переменных в некоторой области.
| "БСЭ" >> "С" >> "СР" >> "СРЕ" >> "СРЕД" |
Статья про "Средние" в Большой Советской Энциклопедии была прочитана 498 раз
| Пицца в сковороде |
| Стейк на сливочном масле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс