


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Тригонометрия
Определение "Тригонометрия" в Большой Советской Энциклопедии
Тригонометрия (от греч. trígōnon - треугольники ¼метрия), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Тригонометрия делится на плоскую, или прямолинейную, и сферическую тригонометрию. Теория тригонометрических функций (гониометрия) и её приложения к решению плоских прямоугольных и косоугольных треугольников изучаются в средней школе.
Основные формулы плоской Тригонометрия Пусть а, b, с - стороны треугольника, А, В, С - противолежащие им углы (А+В+С = p), ha, hb, hc - высоты, 2p - периметр, S - площадь, 2R - диаметр окружности, описанной около треугольника. Теорема синусов: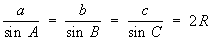 ,
,
теорема косинусов:
a2 = b2 + c2 - 2bc cos A,
теорема тангенсов: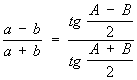 ,
,
площадь треугольника: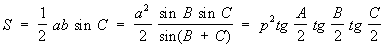 .
.
Углы треугольника, если известны стороны, могут быть найдены по теореме косинусов или по формулам вида: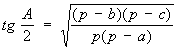 .
.
Плоская Тригонометрия начала развиваться позже сферической, хотя отдельные теоремы её встречались и раньше. Например, 12-я и 13-я теоремы второй книги «Начал» Евклида (3 в. дон. э.) выражают по существу теорему косинусов. Плоская Тригонометрия получила развитие у аль-Баттани (2-я половина 9 - начало 10 вв.), Абу-ль-Вефа (10 в.), Бхаскара (12 в.) и Насирэддина Туси (13 в.), которым была уже известна теорема синусов. Теорема тангенсов была получена Региомонтаном (15 в.). Дальнейшие работы в области Тригонометрия принадлежат Н. Копернику (1-я половина 16 в.), Тригонометрия Браге (2-я половина 16 в.), Ф. Виету (16 в.), И. Кеплеру (конец 16 - 1-я половина 17 вв.). Современный вид Тригонометрия получила в работах Л. Эйлера (18 в.).
Лит.: Кочетков Е. С., Кочеткова Е. С., Алгебра и элементарные функции, ч. 1-2, М., 1966.
| "БСЭ" >> "Т" >> "ТР" >> "ТРИ" >> "ТРИГ" |
Статья про "Тригонометрия" в Большой Советской Энциклопедии была прочитана 718 раз
| Коптим скумбрию в коробке |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная