


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Бесселя неравенство
Определение "Бесселя неравенство" в Большой Советской Энциклопедии
Бесселя неравенство, неравенство для коэффициентов ряда Фурье (см. Фурье ряд) по произвольной ортонормированной системе функций jk (x) (k = 1, 2...), т. е. системе, определённой на некотором отрезке [а, b] и удовлетворяющей условиям (k ¹ l)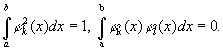
Если функция f (x) измерима на отрезке [а, b], а функция f2(x) интегрируема на этом отрезке и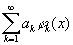
— ряд Фурье f (x) по системе jk (x), то справедливо Бесселя неравенство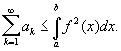
Бесселя неравенство играет важную роль во всех исследованиях, относящихся к теории ортогональных рядов. В частности, оно показывает, что коэффициенты Фурье функции f (x) стремятся к нулю при n ® ¥. Для тригонометрической системы функций это неравенство было получено Ф. Бесселем (1828). Если система функций jk такова, что для любой функции f Бесселя неравенство обращается в равенство, то оно называется Парсеваля равенством.
С. Б. Стечкин.
| "БСЭ" >> "Б" >> "БЕ" >> "БЕС" |
Статья про "Бесселя неравенство" в Большой Советской Энциклопедии была прочитана 691 раз
| Коптим скумбрию в коробке |
| Английская картошка фри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная