


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Фурье интеграл
Определение "Фурье интеграл" в Большой Советской Энциклопедии
Фурье интеграл, формула для разложения непериодической функции на гармонические компоненты, частоты которых пробегают непрерывную совокупность значений. Если функция f (x) удовлетворяет на каждом конечном отрезке условию Дирихле (см. Фурье ряд) и если сходится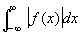 ,
,
то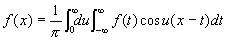 . (1)
. (1)
Эта формула впервые встречается при решении некоторых задач теплопроводности у Ж. Фурье (1811), но её доказательство было дано позже другими математиками. Формулу (1) можно представить также в виде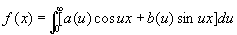 , (2)
, (2)
где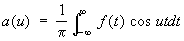 ;
;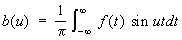 .
.
В частности для чётных функций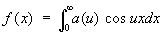 ,
,
где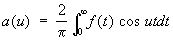 .
.
Формулу (2) можно рассматривать как предельную форму ряда Фурье для функций, имеющих период 2T, когда Т ® ¥. При этом а (u) и b (u) аналогичны коэффициентам Фурье функции f (x). Употребляя комплексные числа, можно заменить формулу (1) формулой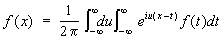 .
.
Формулу (1) можно преобразовать также к виду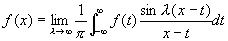 (3)
(3)
(простой интеграл Фурье).
Если интегралы в формулах (2), (3) расходятся (см. Несобственные интегралы), то во многих случаях их можно просуммировать к f (x) при помощи того или иного метода суммирования. При решении многих задач используются формулы Фурье интеграл для функций двух и большего числа переменных.
Лит.: Титчмарш Е., Введение в теорию интегралов Фурье, пер. с англ., М. — Л., 1948.
| "БСЭ" >> "Ф" >> "ФУ" >> "ФУР" |
Статья про "Фурье интеграл" в Большой Советской Энциклопедии была прочитана 798 раз
| Коптим скумбрию в коробке |
| Английское куриное карри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная