


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Целая функция
Определение "Целая функция" в Большой Советской Энциклопедии
Целая функция, функция, аналитическая во всей плоскости комплексного переменного (см. Аналитические функции). Примерами Целая функция могут служить алгебраический многочлен a0 + a1z +... + anzn, функции sinz, cosz, ez. Бесконечно удалённая точка является, вообще говоря, изолированной особой точкой Целая функция Для того чтобы бесконечно удалённая точка была устранимой особой точкой (соответственно полюсом), для Целая функция f (z) необходимо и достаточно, чтобы f (z) была постоянна (соответственно была алгебраическим многочленом). Если точка z = ¥ является существенно особой точкой для Целая функция f (z), то f (z) называют трансцендентной Целая функция Таковы, например, функции sinz, cosz, ez.
Для того чтобы f (z) была Целая функция, необходимо и достаточно, чтобы по крайней мере для одной точки z0 имело место соотношение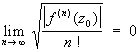
В этом случае разложение f (z) в ряд Тейлора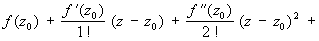
будет сходиться по всей плоскости комплексного переменного.
Основой для классификации трансцендентных Целая функция служит скорость роста М (r) функции, определяемой равенством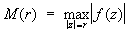
Величину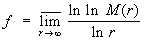
называют порядком Целая функция f (z). В трудах А. Пуанкаре, Ж. Адамара и Э. Бореля была установлена связь между порядком Целая функция и распределением её нулей.
Лит.: Маркушевич А. И., Целые функции, М., 1965.
| "БСЭ" >> "Ц" >> "ЦЕ" >> "ЦЕЛ" |
Статья про "Целая функция" в Большой Советской Энциклопедии была прочитана 785 раз
| Бургер двойного помола |
| Бургер двойного помола |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Объединённая партия гаитянских коммунистов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная