


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Чебышева неравенство
Определение "Чебышева неравенство" в Большой Советской Энциклопедии
Чебышева неравенство,
1) одно из основных неравенств для монотонных последовательностей или функций. В случае конечных последовательностей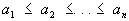
и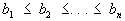
оно имеет вид: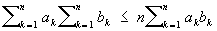
а в интегральной форме ¾ вид: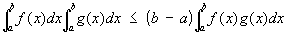 ,
,
где f (x) ³ 0, g (x) ³ 0 и обе функции либо убывают, либо возрастают. Чебышева неравенство установлено П. Л. Чебышевым (1882).
2) Неравенство, дающее оценку вероятности того, что отклонение случайной величины от её математического ожидания превзойдёт некоторую заданную границу. Пусть x — какая-либо случайная величина, Ex = a — её математическое ожидание, а Dx = s2 ¾ её дисперсия. Тогда Чебышева неравенство утверждает, что вероятность неравенства | x ¾ a |³ k s не превосходит величины 1/k2. Если x — сумма независимых случайных величин, то при некоторых дополнительных ограничениях оценка 1/k2 может быть заменена оценкой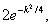
убывающей с ростом k значительно быстрее.
Своё название Чебышева неравенство получило по имени П. Л. Чебышева, который с его помощью установил (1867) весьма широкие условия приложимости закона больших чисел к суммам независимых случайных величин. См. Больших чисел закон, Предельные теоремы теории вероятностей.
| "БСЭ" >> "Ч" >> "ЧЕ" >> "ЧЕБ" |
Статья про "Чебышева неравенство" в Большой Советской Энциклопедии была прочитана 759 раз
| Вкуснейшие куриные леденцы |
| Вкуснейшие куриные леденцы |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная