


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Шаровые функции
Определение "Шаровые функции" в Большой Советской Энциклопедии
Шаровые функции, однородные функции un степени п от прямоугольных координат х, у, z, удовлетворяющие уравнению Лапласа: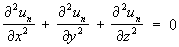
Существуют 2n + 1 линейно-независимых однородных многочленов от х, у, z целой положительной степени n, являющихся Шаровые функции: их линейная комбинация представляет общий вид такого многочлена степени n. Так, например,
uo= a, u1 = ax + by + cz;
u2 = a (x2 - z2) + b (y2 - z2) + cxy + dyz + ezx,
где a, b, с, d, e - произвольные постоянные, представляют общий вид однородных многочленов степеней 0, 1, 2, являющихся Шаровые функции Если вместо прямоугольных координат х, у, z ввести сферические координаты r, q, j, то Шаровые функции выражаются через сферические функции Yп (q,j) по формуле
un = rn Yn (q,j).
Каждой Шаровые функции un степени n соответствует Шаровые функции r ¾2n¾1 степени - n-1.
Шаровые функции применяются при нахождении общего решения уравнения Лапласа и при решении задач математической физики для областей, ограниченных сферическими поверхностями.
Лит. см. при статье Сферические функции.
| "БСЭ" >> "Ш" >> "ША" >> "ШАР" |
Статья про "Шаровые функции" в Большой Советской Энциклопедии была прочитана 1053 раз
| Коптим скумбрию в коробке |
| Коптим скумбрию дома в коробке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная