


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Шрёдингера уравнение
Определение "Шрёдингера уравнение" в Большой Советской Энциклопедии
Шрёдингера уравнение, основное динамическое уравнение нерелятивистской квантовой механики; названо в честь австрийского физика Э. Шрёдингера, который предложил его в 1926. В квантовой механике Шрёдингера уравнение играет такую же фундаментальную роль, как уравнение движения Ньютона в классической механике и Максвелла уравнения в классической теории электромагнетизма. Шрёдингера уравнение описывает измерение во времени состояния квантовых объектов, характеризуемого волновой функцией. Если известна волновая функция y в начальный момент времени, то, решая Шрёдингера уравнение, можно найти y в любой последующий момент времени t.
Для частицы массы т, движущейся под действием силы, порождаемой потенциалом V (х, у, z, t), Шрёдингера уравнение имеет вид: , (1)
, (1)
где i = 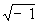 ,
,  = 1,05.10¾27 эрг. сек — Планка постоянная,
= 1,05.10¾27 эрг. сек — Планка постоянная,  — Лапласа оператор (х, у, z — координаты). Это уравнение называется временным Шрёдингера уравнение
— Лапласа оператор (х, у, z — координаты). Это уравнение называется временным Шрёдингера уравнение
Если потенциал V не зависит от времени, то решения Шрёдингера уравнение можно представить в виде:
y(х, у, z, t) =  y (х, у, z), (2)
y (х, у, z), (2)
где Е — полная энергия квантовой системы, а y (x, у, z) удовлетворяет стационарному Шрёдингера уравнение: (3)
(3)
Для квантовых систем, движение которых происходит в ограниченной области пространства, решения Шрёдингера уравнение существуют только для некоторых дискретных значений энергии: E1, E2,..., En,...; члены этого ряда (в общем случае бесконечного) нумеруются набором целых квантовых чисел n. Каждому значению Еп соответствует волновая функция yn (x, у, z), и знание полного набора этих функций позволяет вычислить все измеримые характеристики квантовой системы.
В важном частном случае кулоновского потенциала
(где е — элементарный электрический заряд) Шрёдингера уравнение описывает атом водорода, и En представляют собой энергии стационарных состояний атома.
Шрёдингера уравнение является математическим выражением фундаментального свойства микрочастиц — корпускулярно-волнового дуализма, согласно которому все существующие в природе частицы материи наделены также волновыми свойствами (эта гипотеза впервые была высказана Л. де Бройлем в 1924). Шрёдингера уравнение удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, содержит описание движения частиц по законам классической механики. Переход от Шрёдингера уравнение к классическим траекториям подобен переходу от волновой оптики к геометрической. Аналогия между классической механикой и геометрической оптикой, которая является предельным случаем волновой, сыграла важную роль в установлении Шрёдингера уравнение
С математической точки зрения Шрёдингера уравнение есть волновое уравнение и по своей структуре подобно уравнению, описывающему колебания нагруженной струны. Однако, в отличие от решений уравнения колебаний струны, которые дают геометрическую форму струны в данный момент времени, решения y(х, у, z, t) Шрёдингера уравнение прямого физического смысла не имеют. Смысл имеет квадрат волновой функции, а именно величина rn (x, у, z, t) = |yn (x, у, z, t)|2, равная вероятности нахождения частицы (системы) в момент t в квантовом состоянии n в точке пространства с координатами х, у, z. Эта вероятностная интерпретация волновой функции — один из основных постулатов квантовой механики.
Математическая формулировка постулатов квантовой механики, основанная на Шрёдингера уравнение, носит название волновой механики. Она полностью эквивалентна т. н. матричной механике В. Гейзенберга, которая была сформулирована им в 1925.
Шрёдингера уравнение позволяет объяснить и предсказать большое число явлений атомной физики, а также вычислить основные характеристики атомных систем, наблюдаемые на опыте, например уровни энергии атомов, изменение спектров атомов под влиянием электрического и магнитного полей и т.д. С помощью Шрёдингера уравнение удалось также понять и количественно описать широкий круг явлений ядерной физики, например закономерности a-распада, g-излучение ядер, рассеяние нейтронов на ядрах и др.
Лит.: Шрёдингер Э., Новые пути в физике. Статьи и речи, М., 1971. См. также лит. к ст. Квантовая механика.
Л. И. Пономарёв.
| "БСЭ" >> "Ш" >> "ШР" |
Статья про "Шрёдингера уравнение" в Большой Советской Энциклопедии была прочитана 1205 раз
| Бургер двойного помола |
| Стейк на сливочном масле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная