Библиотека DJVU
БСЭ
Статистика:
Двойное отношение
Значение слова "Двойное отношение" в Большой Советской Энциклопедии
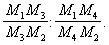
При этом отношение M1M3/M3M2 считается положительным, если направления отрезков M1M3 и M3M2 совпадают, и — отрицательным при различных направлениях. Двойное отношение зависит от порядка нумерации точек, который может отличаться от порядка следования точек на прямой. Наряду с Двойное отношение четырёх точек, рассматривается Двойное отношение четырёх прямых, проходящих через точку О. Это отношение обозначается символом (m1m2m3m4). Оно равно
причём угол (mi mj) между прямыми mi и mj) рассматривается со знаком.
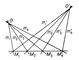
Если точки M1, M2, Мз, M4 лежат на прямых m1, m2, m3, m4 (рис. 1), то
(M1M2M3M4) = (m1m2m3m4),
поэтому, если точки M1, M2, Мз, M4 и M’1, M2’, Мз’, M4’ получены пересечением одной четвёрки прямых m1, m2, m3, m4 (рис. 1), то (M1’, M2’, Мз’, M4’) = (M1M2M3M4).
Если же прямые m1, m2, m3, m4 и m1’, m2’, mз’, m4’ проектируют одну четвёрку точек M1, M2, Мз, M4 (рис. 2), то (m1’ m2’ mз’ m4’) = (m1m2m3m4).
Двойное отношение не меняется также и при любых проективных преобразованиях, т. е. является инвариантом таких преобразований, и поэтому Двойное отношение играют важную роль в проективной геометрии. Особенно важную роль играют четвёрки точек и прямых, для которых Двойное отношение равно — 1. Такие четвёрки называют гармоническими (см. Гармоническое расположение.).
Э. Г. Позняк.
Рис. 1 к ст. Двойное отношение.
Рис. 2 к ст. Двойное отношение.
В Большой Советской Энциклопедии рядом со словом "Двойное отношение"
Буква "Д" | В начало | Буквосочетание "ДВ" |Статья про слово "Двойное отношение" в Большой Советской Энциклопедии была прочитана 0 раз
Интересное