


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Двойной ряд
Определение "Двойной ряд" в Большой Советской Энциклопедии
Двойной ряд, выражение вида
u11 + u12 + ... + u1n + ...
+ u21 + u22 + ... + u2n + ...
....................................
+ um1 + um2 + ... + umn + ...
.....................................,
составленное из элементов бесконечной матрицы ||umn|| (m, n = 1, 2, ...); эти элементы могут быть числами (тогда Двойной ряд называются числовым), функциями от одного или нескольких переменных (функциональный Двойной ряд) и т. д. Для Двойной ряд принята сокращённая запись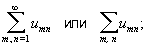
umn называется общим членом Двойной ряд
Конечные суммы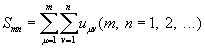
называются частичными суммами Двойной ряд Если существует предел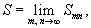
когда m и n независимо друг от друга стремятся к бесконечности, то этот предел называется суммой Двойной ряд и Двойной ряд называются сходящимся. Теория сходимости Двойной ряд значительно сложнее соответствующей теории для простых рядов; например, в отличие от простых рядов, из сходимости Двойной ряд не вытекает, что его частичные суммы ограничены.
Выражение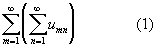
называется повторным рядом. Его надо понимать в том смысле, что сначала вычисляются суммы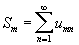
всех внутренних рядов, а затем рассматривается ряд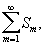
составленный из этих сумм. Если повторный ряд (1) сходится и имеет сумму S, то её называют суммой Двойной ряд по строкам. Аналогично определяется сумма S" Двойной ряд по столбцам. Из сходимости Двойной ряд не вытекает, что сходятся внутренние Ряды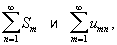
так что суммы по строкам и по столбцам могут и не существовать. Напротив, если Двойной ряд расходится, то может оказаться, что существуют суммы по строкам и по столбцам и S ¹ S". Однако, если Двойной ряд сходится и имеет сумму S и существуют суммы по строкам и по столбцам, то каждая из этих сумм равна S. Это обстоятельство постоянно используется при фактическом вычислении суммы Двойной ряд
Наиболее важными классами Двойной ряд являются двойные степенные ряды, двойные ряды Фурье и квадратичные формы с бесконечным числом переменных. Для Двойной ряд Фурье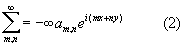
одним из стандартных пониманий суммы таких рядов является следующее: образуются круговые (или сферические) частичные суммы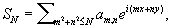
где суммирование распространяется на всевозможные пары целых чисел (m, n), для которых m2 + n2 < N, и рассматривается предел 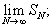 этот предел называется сферической суммой Двойной ряд Фурье (2). Многие важные функции изображаются с помощью Двойной ряд, например эллиптическая функция Вейерштрасса.
этот предел называется сферической суммой Двойной ряд Фурье (2). Многие важные функции изображаются с помощью Двойной ряд, например эллиптическая функция Вейерштрасса.
Кратный ряд (точнее, s-кpaтный ряд) есть выражение вида
Sm, n, …, pumn … q,
составленное из членов таблицы ||umn...p||. Каждый член этой таблицы занумерован s индексами m, n, ..., р, и эти индексы пробегают независимо друг от друга все натуральные числа. Теория кратных рядов совершенно аналогична теории Двойной ряд
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 6 изд., т. 2, М., 1966.
С. Б. Стечкин.
| "БСЭ" >> "Д" >> "ДВ" >> "ДВО" |
Статья про "Двойной ряд" в Большой Советской Энциклопедии была прочитана 712 раз
| Коптим скумбрию в коробке |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная