


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Измерение
Определение "Измерение" в Большой Советской Энциклопедии
Измерение, операция, посредством которой определяется отношение одной (измеряемой) величины к другой однородной величине (принимаемой за единицу); число, выражающее такое отношение, называется численным значением измеряемой величины.
Измерение - одна из древнейших операций, применявшаяся человеком в практической деятельности (при распределении земельных участков, в строительном деле, при ирригационных работах и т. д.); современная хозяйственно-экономическая и общественная жизнь немыслима без Измерение
Для точных наук характерна органическая связь наблюдений и эксперимента с определением численных значений характеристик исследуемых объектов и процессов. Д. Измерение Менделеев не раз подчёркивал, что наука начинается с тех пор, как начинают измерять.
Законченное Измерение включает следующие элементы: объект Измерение, свойство или состояние которого характеризует измеряемая величина; единицу Измерение; технические средства Измерение, проградуированные в выбранных единицах; метод Измерение; наблюдателя или регистрирующее устройство, воспринимающее результат Измерение; окончательный результат Измерение
Простейшим и исторически первым известным видом Измерение является прямое Измерение, при котором результат получается непосредственно из Измерение самой величины (например, Измерение длины проградуированной линейкой, Измерение массы тела при помощи гирь и т. д.). Однако прямые Измерение не всегда возможны. В этих случаях прибегают к косвенным Измерение, основанным на известной зависимости между искомой величиной и непосредственно измеряемыми величинами.
Установленные наукой связи и количественные отношения между различными по своей природе физическими явлениями позволили создать самосогласованную систему единиц, применяемую во всех областях Измерение (см. Международная система единиц).
Измерение следует отличать от других приёмов количественной характеристики величин, применяемых в тех случаях, когда нет однозначного соответствия между величиной и её количественным выражением в определённых единицах. Так, визуальное определение скорости ветра по Бофорта шкале или твёрдости минералов по Мооса шкале следует считать не Измерение, а оценкой.
Всякое Измерение неизбежно связано с погрешностями измерений. Погрешности, порожденные несовершенством метода Измерение, неточной градуировкой и неправильной установкой измерительной аппаратуры, называют систематическими. Систематические погрешности исключают введением поправок, найденных экспериментально. Погрешности другого типа - случайные - обусловлены влиянием на результат Измерение неконтролируемых факторов (ими могут быть, например, случайные колебания температуры, вибрации и т. д.). Случайные погрешности оцениваются методами математической статистики по данным многократных Измерение (см. Наблюдений обработка).
В некоторых случаях - особенно часто встречающихся в атомной и ядерной физике - разброс результатов Измерение связан не только с погрешностями аппаратуры, но и с характером самих исследуемых явлений. Например, если пучок одинаково ускоренных электронов пропустить через щель дифракционной решётки, то электроны с определённой вероятностью попадут в разные точки поставленного за решёткой экрана (см. Дифракция частиц). Приведённый пример показывает, что распространение Измерение на новые области физики требует пересмотра и уточнения понятий, которыми оперируют при Измерение в других областях. С развитием науки и техники возникла ещё одна важная проблема - автоматизация Измерение Это связано, с одной стороны, с условиями, в которых осуществляются современные Измерение (ядерные реакторы, открытый космос и т. д.), с другой стороны - с несовершенством органов чувств человека. В современном производстве, особенно в условиях высоких скоростей, давлений, температур, непосредственное соединение измерительных устройств с регулирующими, минуя человека, позволяет перейти к наиболее совершенной форме производства - автоматизированному производству.
Измерение в метрологии подразделяются на прямые, косвенные, совокупные и совместные. Прямыми называются Измерение, при которых мера или прибор применяются непосредственно для Измерение данной величины (например, Измерение массы на циферблатных или равноплечных весах, Измерение температуры термометром). Косвенными называются Измерение, результаты которых находят на основании известной зависимости между искомой величиной и непосредственно измеряемыми величинами (например, Измерение плотности однородного тела по его массе и геометрическим размерам). Совокупными называются Измерение нескольких одноимённых величин, значения которых находят решением системы уравнений, получаемых в результате прямых Измерение различных сочетаний этих величин (например, калибровка набора гирь, когда значения масс гирь находят на основании прямого Измерение массы одной из них и сравнения масс различных сочетаний гирь). Совместные Измерение - производимые одновременно Измерение двух или нескольких разноимённых величин с целью нахождения зависимости между ними (например, нахождение зависимости удлинения тела от температуры).
Различают также абсолютные и относительные Измерение К первым относят косвенные Измерение, основанные на Измерение одной или нескольких основных величин (например, длины, массы, времени) и использовании значений фундаментальных физических постоянных, через которые измеряемая физическая величина может быть выражена. Под вторыми понимают Измерение либо отношения величины к одноимённой величине, играющей роль произвольной единицы, либо изменения величины относительно другой, принимаемой за исходную.
Найденное в результате Измерение значение измеряемой величины представляет собой произведение отвлечённого числа (числового значения) на единицу данной величины.
Результаты Измерение из-за погрешностей всегда несколько отличаются от истинного значения измеряемой величины, поэтому результаты Измерение обычно сопровождают указанием оценки погрешности (см. Погрешности измерений).
Обеспечение единства Измерение в стране возлагается на метрологическую службу, хранящую эталоны единиц и производящую поверку применяемых средств Измерение Широкое распространение получила классификация Измерение по объектам Измерение Согласно ей, различают Измерение линейные (Измерение длины, площади, объёма), механические (Измерение силы, давления и пр.), электрические и т. д. В общем эта классификация соответствует основным разделам физики.
Лит.: Маликов С. Ф., Тюрин Н. Измерение, Введение в метрологию, 2 изд., М., 1966; Маликов С. Ф., Введение в технику измерений, 2 изд., М., 1952; Яноши Л., Теория и практика обработки результатов измерений, пер. с англ., 2 изд., М., 1968; «Измерительная техника», 1961, № 12: 1962, № 4, 6, 8, 9, 10.
К. П. Широков.
В математической теории Измерение отвлекаются от ограниченной точности физических Измерение Задача Измерение величины Q при помощи единицы меры U состоит в нахождении числового множителя q в равенстве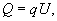 (1)
(1)
при этом Q и U считаются положительными скалярными величинами одного и того же рода (см. Величина), а множитель q - положительное действительное число, которое может быть как рациональным, так и иррациональным. Для рационального q = m/n (m и n - натуральные числа) равенство (1) имеет весьма простой смысл: оно означает, что существует такая величина V (n-я доля от U), которая, будучи взята слагаемым n раз, даёт U, будучи же взята слагаемым m раз, даёт Q :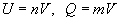 .
.
В этом случае величины Q и U называются соизмеримыми. Для несоизмеримых величин U и Q множитель q иррационален (например, равен числу p, если Q есть длина окружности, а U - её диаметр). В этом случае самое определение смысла равенства (1) несколько сложнее. Можно определить его так: равенство (1) обозначает, что для любого рационального числа r (2)
(2)
Достаточно потребовать, чтобы условие (2) выполнялось для всех десятичных приближений к q по недостатку и по избытку. Следует отметить, что исторически само понятие иррационального числа возникло из задачи Измерение, так что первоначальная задача в случае несоизмеримых величин заключалась собственно не в том, чтобы определить смысл равенства (1), исходя из готовой теории действительных чисел, а в том, чтобы установить смысл символа q, отображающего результат сравнения величины Q с единицей меры U. Например, по определению немецкого математика Р. Дедекинда, иррациональное число есть «сечение» в системе рациональных чисел. Такое сечение и появляется естественно при сравнении двух несоизмеримых величин Q и U. По отношению к этим величинам все рациональные числа разделяются на два класса: класс R1 рациональных чисел r, для которых Q > rU, и класс R2 рациональных чисел r, для которых Q < rU.
Большое значение имеет приближённое Измерение величин при помощи рациональных чисел. Ошибка приближённого равенства Q » rU равна D = (r - qU). Естественно искать такие r = m/n, для которых ошибка меньше, чем при любом числе r" = m’/n’ с знаменателем n" £ n. Такого рода приближения доставляются подходящими дробями r1, r2, r3,... к числу q, которые находятся при помощи теории непрерывных дробей. Например, для длины окружности S, измеряемой диаметром U, приближения таковы: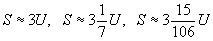
и т. д.; для длины года Q, измеряемой сутками U, приближения таковы: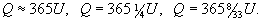
А. Н. Колмогоров.
Измерение в социальном исследовании (в статистике, социологии, психологии, экономике, этнографии), способ упорядочения социальной информации, при котором системы чисел и отношений между ними ставятся в соответствие ряду измеряемых социальных фактов. Различные меры повторяемости, воспроизводимости социальных фактов и являются социальными измерениями, или шкалами. С развитием общества получают распространение простые шкалы - денежная оценка труда, разряды квалификации, оценка успехов в обучении (система баллов), спорте и др. Измерение в общественных науках отличается от таких «естественных» шкал точным определением измеряемых признаков и правил построения шкалы.
В социальных исследованиях Измерение впервые вошли в употребление в 1920-30, когда исследователи столкнулись с проблемой достоверности при изучении общественного сознания, социально-психологических установок (отношений), социального и профессионального статусов, общественного мнения, качественных характеристик условий труда и быта и т. д. Эти Измерение являются примером стандартизованной групповой оценки, когда с помощью методов выборочной статистики измеряется «интенсивность» общественного мнения.
Измерение разделяются на три типа: 1) номинальное - числа, приписываемые объектам на номинальной шкале, лишь констатируют отличие или тождество этих объектов, т. е. номинальная шкала есть, по существу, группировка или классификация. 2) порядковое - числа, приписываемые объектам на шкале, упорядочивают их по измеряемому признаку, но указывают лишь на порядок размещения объектов на шкале, а не на расстояние между объектами или, тем более, координаты; 3) интервальное - числа, приписываемые объектам на шкале, указывают не только на порядок объектов, но и на расстояние между ними. Интервальным Измерение является, например, шкала привлекательности профессий. Такая шкала, придавая каждой профессии условный балл, позволяет сравнивать профессии по популярности, т. е. утверждать, что, например, профессия шофёра на М баллов популярнее профессии слесаря и на К баллов менее популярна, чем профессия лётчика. Однако она не позволяет утверждать, что интерес к профессиям шофёра и слесаря превышает интерес к профессии лётчика, если сумма соответствующих баллов превышает балл профессии лётчика. Нахождение количественной меры социальных явлений и процессов ограничивается этими тремя типами Измерение Предпринимаются попытки создания четвёртого типа Измерение - количественного, с введением единицы Измерение
Лит.: Ядов В. А., Методология и процедуры социологических исследований, Тарту, 1968; Здравомыслов А. Г., Методология и процедура социологических исследований, М., 1969.
Ю. Б. Самсонов.
| "БСЭ" >> "И" >> "ИЗ" >> "ИЗМ" |
Статья про "Измерение" в Большой Советской Энциклопедии была прочитана 903 раз
| Коптим скумбрию в коробке |
| Английское куриное карри |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная