


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Квадратичное отклонение
Определение "Квадратичное отклонение" в Большой Советской Энциклопедии
Квадратичное отклонение, квадратичное уклонение, стандартное отклонение величин x1, x2,..., xn от а - квадратный корень из выражения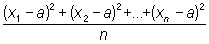 .
.
Наименьшее значение Квадратичное отклонение имеет при а = 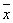 , где
, где 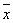 - среднее арифметическое величин x1, x2,..., xn:
- среднее арифметическое величин x1, x2,..., xn: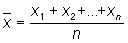 .
.
В этом случае Квадратичное отклонение может служить мерой рассеяния системы величин x1, x2,..., xn. Употребляют также более общее понятие взвешенного Квадратичное отклонение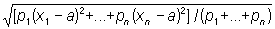 ;
;
числа p1,..., pn называют при этом весами, соответствующими величинам x1,..., xn. Взвешенное Квадратичное отклонение достигает наименьшего значения при а, равном взвешенному среднему:
(p1x1 +... + pnxn)/(p1 +...+ pn).
В теории вероятностей Квадратичное отклонение ох случайной величины Х (от её математического ожидания) называют квадратный корень из дисперсии 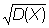 .
.
Квадратичное отклонение употребляют как меру качества статистических оценок и называют в этом случае квадратичной ошибкой. См. Ошибок теория.
| "БСЭ" >> "К" >> "КВ" >> "КВА" >> "КВАД" |
Статья про "Квадратичное отклонение" в Большой Советской Энциклопедии была прочитана 931 раз
| Коптим скумбрию в коробке |
| Гороховое пюре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная