


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Конечных разностей исчисление
Определение "Конечных разностей исчисление" в Большой Советской Энциклопедии
Конечных разностей исчисление, раздел математики, в котором изучаются функции при дискретном (прерывном) изменении аргумента, в отличие от дифференциального исчисления и интегрального исчисления, где аргумент предполагается непрерывно изменяющимся. Конечными разностями «вперёд» для последовательности значений y1= f (x1), y2 = f (x2),..., yk = f (xk),... функции f (x), соответствующих последовательности значений аргумента x0,..., xk,,... (xk = х0 + kh, h — постоянное, k — целое), называют выражения:
Dyk º Df (xk) = f (xk+1) - f (xk)
(разности 1-го порядка),
D2yk º D2f (xk) = Df (xk+1)- Df (xk) = f (xk+2)-2f (xk+1) + f (xk)
(разности 2-го порядка),
Dnyk º Dnf (xk) = Dn-1f (xk+1) - Dn-1f (xk)
(разности n-го порядка).
Соответственно, конечные разности «назад» Dnyк определяются равенствами
Dnyк = Dnyк + n.
При интерполяции часто пользуются т. н. центральными разностями dny, которые вычисляются при нечётном n в точках х = xi+1l2h, а при чётном n в точках х = xi по формулам
df (xi + 1/2h) º dyi+1/2 = f (xi+1) - f (xi),
d2f (xi) º d2yi = dyi+1/2,
d2m-1f (xi + 1/2h) º d2т—1yi+1/2 = d2т—2yi+1-d2т—2yi,
d2mf (xi) º d2туi = d2т—1yi+1/2 - d2т—1yi-1/2
Они дополняются средними арифметическими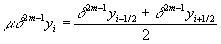 ,
,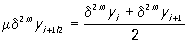 ,
,
где m = 1,2,...; если m = 0, то полагают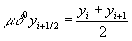 .
.
Центральные разности dny связаны с конечными разностями Dny соотношениями
d2туi = D2туi-m,
d2т+1yi+1/2 = D2m+1yi-m
Если значения аргумента не составляют арифметической прогрессии, т. е. xk+1 - xk не есть тождественно постоянная, то вместо конечных разностей пользуются разделёнными разностями, последовательно определяемыми по формулам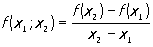
…………………………..……………………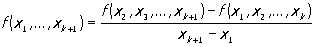 .
.
Связь между конечными разностями и производными устанавливается формулой Dnyk = f (n)(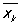 ), где xk£
), где xk£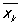 £xk+n. Существует полная аналогия между ролью конечных разностей в теории функций дискретного аргумента и ролью производных в теории функций непрерывного аргумента; конечные разности являются удобным аппаратом при построении ряда разделов численного анализа: интерполирование функций, численное дифференцирование и интегрирование, численные методы решения дифференциальных уравнений.
£xk+n. Существует полная аналогия между ролью конечных разностей в теории функций дискретного аргумента и ролью производных в теории функций непрерывного аргумента; конечные разности являются удобным аппаратом при построении ряда разделов численного анализа: интерполирование функций, численное дифференцирование и интегрирование, численные методы решения дифференциальных уравнений.
Например, для приближённого решения дифференциального уравнения (обыкновенного или с частными производными) часто заменяют входящие в него производные соответствующими разностями, деленными на степени разностей аргументов, и решают полученное таким способом разностное уравнение (одномерное или многомерное).
Важный раздел Конечных разностей исчисление посвящен решению разностных уравнений вида
F [x,(f (x),...,Dnf (x)] = 0 (1)
задаче, во многом сходной с решением дифференциальных уравнений n-го порядка. Обычно уравнение (1) записывают в виде
Ф [х, f (x), f (x1),..., f (xn)] = 0,
выражая разности через соответствующие значения функции. Особенно простой случай представляет линейное однородное уравнение с постоянными коэффициентами:
f (x+n) + a1f (x+n-1) +... + anf (x) = 0,
где a1,..., an — постоянные числа. Чтобы решить такое уравнение, находят корни l1, l2,... ln его характеристического уравнения
ln + a1ln-1+...+an = 0.
Тогда общее решение данного уравнения представится в виде
f (x) = С1l1х + C2l2x +... + Cnlnx,
где C1, C2,..., Cn — произвольные постоянные (здесь предполагается, что среди чисел l1, l2,..., ln нет равных).
Лит.: Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1—2, М., 1966; Гельфонд А. О., Исчисление конечных разностей, 3 изд., М., 1967.
Под редакцией Н. С. Бахвалова.
| "БСЭ" >> "К" >> "КО" >> "КОН" >> "КОНЕ" |
Статья про "Конечных разностей исчисление" в Большой Советской Энциклопедии была прочитана 719 раз
| Пицца в сковороде |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная