Математические развлечения и игры

Определение "Математические развлечения и игры" в Большой Советской Энциклопедии

Математические развлечения и игры. Рис.

Математические развлечения и игры. Математическими развлечениями называют обычно разнообразные задачи и упражнения занимательного характера, требующие проявления находчивости, смекалки, оригинальности мышления, умения критически оценить условия или постановку вопроса: в частности — головоломки, задачи на превращение одной фигуры в другую путём разрезания и переложения частей, фокусы, основанные на вычислениях, математические игры. К математическим играм относят либо игры, имеющие дело с числами, фигурами и тому подобным, либо игры, исход которых может быть предопределён предварительным теоретическим анализом. С появлением и развитием математических игр теории термин «математические игры» (в смысле этой статьи) постепенно выходит из употребления.

Математические развлечения и игры. Рис.

Игра Баше. Из кучки, содержащей n (например, 35) предметов, двое играющих берут поочерёдно не более чем по m (например, 5) предметов. Выигрывает тот, кто возьмёт последние предметы. Теория игры устанавливает, что если n не делится на m + 1, то начинающий игру непременно выиграет, если каждый раз будет оставлять партнёру число предметов, кратное m + 1 (в примере — кратное 6).

Математические развлечения и игры. Рис.

Игра «15». Играет один человек. На шестнадцатиклеточной доске расположены в случайном порядке 15 перенумерованных шашек. Передвигая шашку одну за другой на свободную клетку с любой из смежных с ней клеток, требуется упорядочить расположение шашек (привести к нормальному расположению — положению 1, указанному на рисунке 1). Теоретический анализ игры, известный с 1879, показывает, что задача может быть решена только в том случае, если число инверсий (то есть число нарушений нормального расположения), образуемых номерами шашек в исходном положении, имеет ту же чётность, что и номер строки, в которой есть свободная клетка. Чтобы установить число инверсий, надо для каждой шашки подсчитать число предшествующих ей шашек с большим номером и сложить все эти числа; их сумма и равна искомому числу инверсий. При этом устанавливается следующая последовательность в исходном расположении шашек: слева направо вдоль строк и сверху вниз при переходе от одной строки к другой. Например, в расположении II (рис. 1) число инверсий чётно (равно 38), а свободная клетка находится в чётной (во 2-й) строке, то есть расположение II может быть приведено к нормальному. Напротив, расположение III привести к нормальному невозможно, так как число инверсий в нём нечётно (равно 1: шашка с № 15 предшествует шашке с № 14), а свободная клетка находится в 4-й строке (в строке с чётным номером).

Полное математическое обоснование имеется также у таких М. р. и и., как вычерчивание фигур одним росчерком, лабиринты, комбинированные задачи на шахматной доске и другие. Большая группа М. р. и и. связана с поисками оригинальных и красивых решений задач, допускающих практически неисчерпаемое или даже бесконечное множество решений.

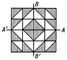
К числу таких развлечений относится, например, «составление паркетов» — задача о заполнении плоскости правильно чередующимися фигурами одного и того же вида (например, одноимёнными правильными многоугольниками) или нескольких данных видов. Если «двухцветный квадратный паркет» с осями симметрии А’ А и B’B (см. рис. 2) составляется из 4n² равных квадратов, каждый из которых разбит диагональю на белую и чёрную половины, то число различных паркетов равно 4n² (это число быстро растет при возрастании n).

Очень большое, до сих пор точно не установленное число решений имеют также: задача Эйлера о шахматном коне — обойти ходом коня шахматную доску, побывав на каждой клетке по одному разу, и задача о составлении многоклеточных магических квадратов. В подобного рода задачах интересуются обычно определением числа решений, разработкой методов, дающих сразу большие группы решений. Математическое содержание ряда других М. р. и и. — в установлении наименьшего числа операций, необходимых для достижения поставленной цели. К таким развлечениям относятся: задачи типа «переправ», «размещений» или игры, аналогичные игре «ханойская башня», суть которой в подсчёте числа ходов, необходимых для перенесения пластинок со столбика А (см. рис. 3) на столбик С, пользуясь столбиком В, если за один ход можно переносить лишь одну пластинку с любого столбика на любой другой, но нельзя класть большую пластинку выше меньшей.

М. р. и и. пользовались вниманием многих крупных учёных [Леонардо Пизанский (13 век), Н. Тарталья (16 век), Дж. Кардано (16 век), Г. Монж (2-я половина 18 — начало 19 века), Л. Эйлер (18 век) и другие]. Сборники М. р. и и. начали появляться с 17 века. Содействуя повышению интереса учащихся к математике, развитию сообразительности, настойчивости и внимания, М. р. и и. применяются также и в педагогическом процессе. В России это нашло отражение уже в «Арифметике» Л. Ф. Магницкого (1703) и даже в математических рукописях 17 века.

Лит.: Игнатьев Е. И., В царстве смекалки или арифметика для всех, 2 изд., кн. 1—3, М. — Л., 1924 — 25; Кордемский Б. А., Математическая смекалка, 8 изд., М., 1965; Перельман Я. И., Живая математика, 9 изд., М., 1970: его же, Занимательная арифметика, 9 изд., М., 1959; его же, Занимательная алгебра, 12 изд., М., 1970; его же, Занимательная геометрия, 11 изд., М., 1959; Шуберт Г., Математические развлечения и игры, перевод с немецкого, Одесса, 1911; Арене В., Математические игры, перевод с немецкого, Л. — М., 1924; Гарднер М., Математические чудеса и тайны. Математические фокусы и головоломки, перевод с английского, 2 изд., М., 1967; его же, Математические досуги, перевод с английского, М., 1972.