


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Архимед
Определение "Архимед" в Большой Советской Энциклопедии
 |
| Архимед |
Архимед родился в Сиракузах (о. Сицилия) и жил в этом городе в эпоху 1-й и 2-й Пунических войн. Предполагают, что он был сыном астронома Фидия. Научную деятельность начал как механик и техник. Архимед совершил поездку в Египет и сблизился с александрийскими учёными, в том числе с Кононом и Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. Архимед был близок к сиракузскому царю Гиерону II. Во время 2-й Пунической войны Архимед организовал инженерную оборону Сиракуз от римских войск. Его военные машины заставили римлян отказаться от попыток взять город штурмом и вынудили их перейти к длительной осаде. При взятии города войсками Марцелла Архимед был убит римским солдатом, которого, по преданию, встретил словами «не трогай моих чертежей». На могиле Архимед был поставлен памятник с изображением шара и описанного около него цилиндра. Эпитафия указывала, что объёмы этих тел относятся, как 2:3 - открытие Архимед, которое он особенно ценил.
Работы Архимед показывают, что он был прекрасно знаком с математикой и астрономией своего времени, и поражают глубиной проникновения в существо рассматриваемых Архимед задач. Ряд работ имеет вид посланий к друзьям и коллегам. Иногда Архимед предварительно сообщал им без доказательств свои открытия, с тонкой иронией добавляя несколько неверных предложений.
В 9-11 вв. работы Архимед переводились на арабский язык, с 13 в. они появляются в Зап. Европе в латинском переводе. С 16 в. начинают выходить печатные издания Архимед, в 17-19 вв. они переводятся на новые языки. Первое издание отдельных трудов Архимед на русском языке относится к 1823. Некоторые работы Архимед до нас не дошли или известны лишь в отрывках, а его «Послание к Эратосфену» было найдено лишь в 1906.
Центральной темой математических работ Архимед являются задачи на нахождение площадей поверхностей и объёмов. Решение многих задач этого типа Архимед первоначально нашёл, применяя механические соображения, по существу сводящиеся к методу «неделимых» (см. «Неделимых» метод), а затем строго доказал методом исчерпывания (см. Исчерпывания метод), который он значительно развил. Рассмотрение Архимед двусторонних оценок погрешности при проведении интеграционных процессов позволяет считать его предшественником не только И. Ньютона и Г. Лейбница, но и Г. Римана. Архимед вычислил площадь эллипса, параболического сегмента, нашёл площадь поверхности конуса и шара, объём шара и сферического сегмента, а также различных тел вращения и их сегментов. Архимед исследовал свойства т. н. архимедовой спирали. Дал построение касательной к этой спирали, нашёл площадь её витка. Здесь он выступает как предшественник методов дифференциального исчисления. Архимед рассмотрел также одну задачу изопериметрического типа. В ходе своих исследований он нашёл сумму бесконечной геометрической прогрессии со знаменателем 1/4, что явилось первым примером появления в математике бесконечного ряда. При исследовании одной задачи, сводящейся к кубическому уравнению, Архимед выяснил роль характеристики, которая позже получила название дискриминанта. Архимед принадлежит формула для определения площади треугольника через 3 его стороны (неправильно именуемая формулой Герона). Архимед дал (не вполне исчерпывающую) теорию полуправильных выпуклых многогранников (архимедовы тела). Особое значение имеет аксиома Архимеда (см. Архимеда аксиома): из неравных отрезков меньший, будучи повторен достаточное число раз, превзойдёт больший. Эта аксиома определяет т. н. архимедовскую упорядоченность, которая играет важную роль в современной математике. Архимед построил счисление, позволяющее записывать и называть весьма большие числа. Он с большой точностью вычислил значение числа p и указал пределы погрешности: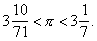
Механика постоянно находилась в круге интересов Архимед В одной из своих первых работ он исследует распределение нагрузок между опорами балки. Архимед принадлежит определение понятия центра тяжести тела. Применяя, в частности, интеграционные методы, он нашёл положение центра тяжести различных фигур и тел. Архимед дал математический вывод законов рычага. Ему приписывают гордую фразу: «Дай мне, где стать, и я сдвину Землю». Архимед заложил основы гидростатики. Он сформулировал основные положения этой дисциплины, в том числе знаменитый закон Архимед (см. Архимеда закон). Последняя работа Архимед посвящена исследованию равновесия плавающих тел. При этом он выделяет устойчивые положения равновесия. Архимед изобрёл водоподъёмный механизм, т. н. архимедов винт (см. Водоподъёмная машина), который явился прообразом корабельных, а также воздушных винтов. Рассказывают, что Архимед нашёл решение задачи об определении количества золота и серебра в жертвенной короне Гиерона, когда садился в ванну, и нагим побежал домой с криком «эврика!» («нашёл!»). Архимед занимался также астрономией. Он сконструировал прибор для определения видимого (углового) диаметра Солнца и нашёл значение этого угла с поразительной точностью. При этом Архимед вводил поправку на размер зрачка. Он первым стал приводить наблюдения к центру Земли. Наконец, Архимед построил небесную сферу - механический прибор, на котором можно было наблюдать движения планет, фазы Луны, солнечные и лунные затмения.
Соч.: Archimedis opera omnia cum commentariis Eutocii, ed. J. L. Heiberg, v. 1-3, Lipsiae, 1910-15; в рус. пер. - Сочинения, М., 1962 (библ. с. 635-37).
Лит.: Чвалина Архимед, Архимед, пер. с нем., М.-Л., 1934; Лурье С. Я., Архимед, М.-Л., 1945; Каган В. Ф., Архимед. Краткий очерк о жизни и творчестве, М.-Л., 1949; Веселовский И. Н., Архимед, М., 1957; Heath Т. L., Archimedes, L., 1920.
С. Б. Стечкин.
| "БСЭ" >> "А" >> "АР" >> "АРХ" >> "АРХИ" |
Статья про "Архимед" в Большой Советской Энциклопедии была прочитана 952 раз
| Коптим скумбрию в коробке |
| Кукурузный крем суп со скатом |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Объединённая партия гаитянских коммунистов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Балкано-кавказская раса
- «Сообразительный»
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная