


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Нормированное кольцо
Определение "Нормированное кольцо" в Большой Советской Энциклопедии
Нормированное кольцо, важное понятие функционального анализа, значительно расширившее область его приложений. Элементы Нормированное кольцо являются одновременно и точками некоторого геометрического образования - полного нормированного пространства, и элементами некоторого алгебраического образования - кольца, в котором определено ещё умножение на числа (причём алгебраические операции непрерывны по норме). Примерами Нормированное кольцо могут служить: кольцо С всех непрерывных функций на отрезке [0,1] с обычными алгебраическими операциями и нормой 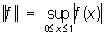 , кольцо L1 всех абсолютно интегрируемых на прямой функций, в котором умножение определено как свёртывание:
, кольцо L1 всех абсолютно интегрируемых на прямой функций, в котором умножение определено как свёртывание: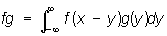 ,
, 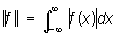 ;
;
кольцо матриц n-го порядка; кольцо ограниченных операторов гильбертова пространства - кольцо операторов, и т.д. Наиболее разработана теория коммутативных Нормированное кольцо (т. е. Нормированное кольцо, в которых умножение перестановочно: ху = ух), созданная И. М. Гельфандом.
Наряду с термином «Нормированное кольцо» употребляется термин «банахова алгебра».
Лит.: Наймарк М. А., Нормированные кольца, М., 1956.
| "БСЭ" >> "Н" >> "НО" >> "НОР" >> "НОРМ" |
Статья про "Нормированное кольцо" в Большой Советской Энциклопедии была прочитана 521 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Объединённая партия гаитянских коммунистов
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная