Огибающая

Значение слова "Огибающая" в Большой Советской Энциклопедии

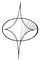Огибающая семейства линий на плоскости (поверхностей в пространстве), линия (поверхность), которая в каждой своей точке касается одной линии (поверхности) семейства, геометрически отличной от Огибающая в сколь угодно малой окрестности точки касания (см. Семейство линий, Семейство поверхностей). Уравнение Огибающая семейства линий на плоскости, определяемого уравнением f (х, у, С) = 0, содержащим параметр С, можно получить [в предположении, что f (х, у, С) имеет непрерывные частные производные 1-го порядка по всем трём аргументам], исключив параметр С из системы:

f (x, у, С) = 0, f "_c (х, у, С) = 0.

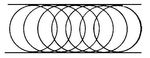Это исключение, вообще говоря, даёт не только Огибающая, но и геометрическое место особых точек линий семейства, т. е. точки, для которых одновременно f "_x = 0, f "_y = 0.

Примеры (на плоскости): а) семейство окружностей радиуса R, центры которых лежат на одной прямой, имеет в качестве Огибающая пару прямых, параллельных линии центров и отстоящих от неё в ту и другую сторону на расстояние R (см. рис. 1); б) всякая кривая служит Огибающая для семейства своих касательных и семейства своих кругов кривизны; в) если в каждой точке кривой построить к ней нормаль, то для полученного семейства прямых Огибающая будет эволюта (см. Эволюта и эвольвента) данной кривой (на рис. 2 изображена эволюта эллипса).

В пространстве для семейств поверхностей могут существовать Огибающая, касающиеся поверхностей семейства в точках или же вдоль некоторых линий. Примеры: а) семейство сфер радиуса R с центрами, расположенными на одной прямой, имеет своей Огибающая круглый цилиндр радиуса R, ось которого есть линия центров (касание цилиндра с каждой сферой — по окружности); б) семейство сфер радиуса R, центры которых лежат в одной плоскости, имеет Огибающая пару плоскостей, параллельных плоскости центров и отстоящих от неё в ту и другую сторону на расстояние R (касание плоскостей каждой сферой — точке).

Понятие Огибающая имеет значение не только в геометрии, но и в некоторых вопросах математического анализа (особые решения в теории дифференциальных уравнений), теоретической физики (в оптике — каустика, фронт волны).

Лит.: Толстов Г. П., К отысканию огибающей семейства плоских кривых, «Успехи математических наук», 1952, т. 7, в. 4; Ла Валле-Пуссен Ш.-Ж. де, Курс анализа бесконечно малых, пер. с франц., т. 2, Л. — М., 1933; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.

Рис. 1 к ст. Огибающая.

Рис. 2 к ст. Огибающая.

В Большой Советской Энциклопедии рядом со словом "Огибающая"

Ахмат | Буква "О" | В начало | Буквосочетание "ОГ" | ОГИЗ

Статья про слово "Огибающая" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

Florists in america

business support in USA