


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Остроградского метод
Определение "Остроградского метод" в Большой Советской Энциклопедии
Остроградского метод, метод выделения рациональной части неопределённого интеграла
где Q (x) — многочлен степени п, имеющий кратные корни, а Р (х) — многочлен степени m £ n — 1.
Остроградского метод позволяет алгебраическим путём представить такой интеграл в виде суммы двух слагаемых, из которых первое является рациональной функцией переменного х, а второе рациональной части не содержит. Имеет место равенство (1)
(1)
где Q1, Q2, P1, P2 — многочлены степеней соответственно n1, n2, m1, m2, причём n1 + n2= n, m1 £ n1 — 1, m2 £ n2 — 1 и многочлен Q2(x) не имеет кратных корней. Многочлен Q1(x) является наибольшим общим делителем многочленов Q (x) и 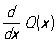 , и, следовательно, явное выражение Q1(x) можно найти, например, с помощью Евклида алгоритма. Дифференцируя правую и левую части (1), получим тождество
, и, следовательно, явное выражение Q1(x) можно найти, например, с помощью Евклида алгоритма. Дифференцируя правую и левую части (1), получим тождество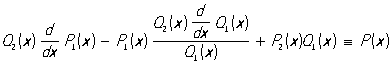 . (2)
. (2)
Тождество (2) позволяет найти явное выражение многочленов P1(x) и P2(x) неопределённых коэффициентов методом.
Остроградского метод был впервые предложен в 1844 М. В. Остроградским.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.
| "БСЭ" >> "О" >> "ОС" >> "ОСТ" >> "ОСТР" |
Статья про "Остроградского метод" в Большой Советской Энциклопедии была прочитана 755 раз
| Пицца в сковороде |
| Кукурузный крем суп со скатом |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная