Параболоиды

Определение "Параболоиды" в Большой Советской Энциклопедии

Гиперболический параболоид

Параболоиды (от парабола и греч. éidos — вид), незамкнутые поверхности второго порядка, не имеющие центра. Различают два вида Параболоиды: эллиптический Параболоиды (рис. 1) и гиперболический Параболоиды (рис. 2). Параболоиды представляют собой два типа из общего числа пяти основных типов поверхностей второго порядка. Линиями пересечения гиперболического Параболоиды со всевозможными плоскостями пространства являются гиперболы, параболы и прямые. Через каждую точку гиперболического Параболоиды проходят две прямолинейные образующие, и, таким образом, гиперболический Параболоиды представляет собой линейчатую поверхность. Для эллиптического Параболоиды существуют плоскости, не пересекающиеся с ним. Если же плоскость пересекается с эллиптическим Параболоиды, то линией пересечения является либо эллипс, либо парабола. В надлежащей системе координат уравнения Параболоиды имеют вид:
x²/2p + y²/2q = z (эллиптический Параболоиды),
x²/2p — y²/2q = z (гиперболический Параболоиды);
здесь р > 0 и q > 0.

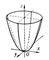Эллиптический параболоид