


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Первый интеграл
Определение "Первый интеграл" в Большой Советской Энциклопедии
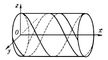 |
| Первый интеграл. Рис. |
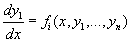 , i = 1, …, n
, i = 1, …, n- соотношение вида
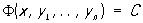
(где С - произвольная постоянная), левая часть которого сохраняет постоянное значение при подстановке любого решения y1 = y1(x),..., yn= yn (x) системы, но не является тождественной постоянной (см. Дифференциальные уравнения). Геометрически Первый интеграл представляет собой семейство гиперповерхностей в (n + 1)-мерном пространстве Oxy1... yn, на каждой из которых расположено некоторое подсемейство интегральных кривых системы. Например, одним из Первый интеграл системы 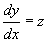 ,
, 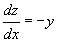 является y2 + x2 = C2 (круговые цилиндры); интегральные кривые у = Csin (x - x0), z = Ccos (x-x0) суть винтовые линии, расположенные на этих цилиндрах (см. рис.). Если известно k независимых Первый интеграл Фi (x1, y1,..., уп) = Ci (i = 1,..., k; k < n) системы, то её порядок, вообще говоря, может быть понижен на k единиц; если k = n, то общий интеграл системы получается без интегрирования.
является y2 + x2 = C2 (круговые цилиндры); интегральные кривые у = Csin (x - x0), z = Ccos (x-x0) суть винтовые линии, расположенные на этих цилиндрах (см. рис.). Если известно k независимых Первый интеграл Фi (x1, y1,..., уп) = Ci (i = 1,..., k; k < n) системы, то её порядок, вообще говоря, может быть понижен на k единиц; если k = n, то общий интеграл системы получается без интегрирования.
Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959.
| "БСЭ" >> "П" >> "ПЕ" >> "ПЕР" >> "ПЕРВ" |
Статья про "Первый интеграл" в Большой Советской Энциклопедии была прочитана 625 раз
| Коптим скумбрию в коробке |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная