


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Прямоугольников формула
Определение "Прямоугольников формула" в Большой Советской Энциклопедии
Прямоугольников формула, простейшая формула для приближённого вычисления определённого интеграла, имеющая вид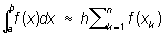
где h = (b — a)/n, xk = x + (k — 1) h и a £ x £ a + h. Наиболее точной из всех Прямоугольников формула является формула средних ординат, в которой x = а + h/2; если ÷f "" (x)÷ < М на отрезке [а, b], то для этой формулы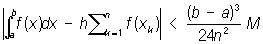
Остальные Прямоугольников формула в общем случае менее точны; поэтому, например, вместо формул, в которых x = а и x = а + h, предпочитают пользоваться их средним арифметическим (см. Трапеций формула), т.к. погрешность при этом будет не больше (b — a)3M/12n2. Если обе части Прямоугольников формула для x = а + h/2, x = а и x = а + h умножить соответственно на коэффициенты 2/3, 1/6, и 1/6, а затем сложить, то получится более точная формула приближённого интегрирования (см. Симпсона формула), погрешность которой не больше (b — a)5N/2880n 4, где N — максимум úf IV (x)ú на отрезке [а, b].
| "БСЭ" >> "П" >> "ПР" >> "ПРЯ" |
Статья про "Прямоугольников формула" в Большой Советской Энциклопедии была прочитана 677 раз
| Коптим скумбрию в коробке |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная