


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Пуассона распределение
Определение "Пуассона распределение" в Большой Советской Энциклопедии
 |
| Пуассона распределение. Рис. |
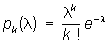 , k = 0, 1, 2,...
, k = 0, 1, 2,...(l — положительный параметр). Своё название «Пуассона распределение» получило по имени С. Д. Пуассона (1837). Математическое ожидание и дисперсия случайной величины, имеющей Пуассона распределение с параметром l, равны l. Если независимые случайные величины X1 и X2 имеют Пуассона распределение с параметрами l1 и l2, то их сумма X1 + X2 имеет Пуассона распределение с параметрами l1 + l2.
В теоретико-вероятностных моделях Пуассона распределение используется как аппроксимирующее и как точное распределение. Например, если при n независимых испытаниях события A1,..., An осуществляются с одной и той же малой вероятностью р, то вероятность одновременного осуществления каких-либо k событий (из общего числа n) приближённо выражается функцией pk (np) (математическое содержание этого утверждения при больших значениях n и 1/р формулируются Пуассона теоремой). В частности, такая модель хорошо описывает процесс радиоактивного распада и многие др. физические явления.
Как точное Пуассона распределение появляется в теории случайных процессов. Например, при расчёте нагрузки линий связи обычно предполагают, что количества вызовов, поступивших за непересекающиеся интервалы времени, суть независимые случайные величины, подчиняющиеся Пуассона распределение с параметрами, значения которых пропорциональны длинам соответствующих интервалов времени (см. Пуассоновский процесс).
В качестве оценки неизвестного параметра l по n наблюдённым значениям независимых случайных величин X1,..., Xn используется их арифметическое среднее X = (X1 +... + Xn)/n, поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально (см. Статистические оценки).
Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М. — Л., 1969; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.
| "БСЭ" >> "П" >> "ПУ" >> "ПУА" |
Статья про "Пуассона распределение" в Большой Советской Энциклопедии была прочитана 711 раз
| Семга на горелке |
| Семга на горелке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная