


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Статистические оценки
Определение "Статистические оценки" в Большой Советской Энциклопедии
Статистические оценки, функции от результатов наблюдений, употребляемые для статистического оценивания неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X1,..., Xn - независимые случайные величины, имеющие одно и то же нормальное распределение с неизвестным средним значением а, то функции - среднее арифметическое результатов наблюдений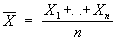
и выборочная медиана m = m(X1,..., Xn) являются возможными точечными Статистические оценки неизвестного параметра а. В качестве Статистические оценки какого-либо параметра q естественно выбрать функцию q*(X1,..., Xn) от результатов наблюдений X1,..., Xn, в некотором смысле близкую к истинному значению параметра. Принимая какую-либо меру «близости» Статистические оценки к значению оцениваемого параметра, можно сравнивать различные оценки по качеству. Обычно мерой близости оценки к истинному значению параметра служит величина среднего значения квадрата ошибки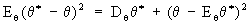
(выражающаяся через математическое ожидание оценки E0q* и её дисперсию D0q*). В классе всех несмещённых оценок (для которых E0q* = 0) наилучшими с этой точки зрения будут оценки, имеющие при заданном n минимальную возможную дисперсию при всех q. Указанная выше оценка Х для параметра а нормального распределения является наилучшей несмещенной оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра а удовлетворяет неравенству 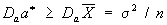 , где s2 - дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики. Имея в виду построение Статистические оценки для больших значений n, естественно предполагать, что вероятность отклонений q* от истинного значения параметра q, превосходящих какое-либо заданное число, будет близка к нулю при n ®¥. Статистические оценки с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n ®¥, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение Статистические оценки производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере - наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а, тогда как выборочная медиана m, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к.
, где s2 - дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики. Имея в виду построение Статистические оценки для больших значений n, естественно предполагать, что вероятность отклонений q* от истинного значения параметра q, превосходящих какое-либо заданное число, будет близка к нулю при n ®¥. Статистические оценки с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n ®¥, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение Статистические оценки производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере - наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а, тогда как выборочная медиана m, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к. 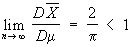
(тем не менее использование m имеет также положительные стороны: например, если истинное распределение не является в точности нормальным, а несколько отличается от него, дисперсия Х может резко возрасти, а дисперсия m остаётся почти той же, т. е. m обладает свойством, называется «прочностью»). Одним из распространённых общих методов получения Статистические оценки является метод моментов, который заключается в приравнивании определённого числа выборочных моментов к соответствующим моментам теоретического распределения, которые суть функции от неизвестных параметров, и решении полученных уравнений относительно этих параметров. Хотя метод моментов удобен в практическом отношении, однако Статистические оценки, найденные при его использовании, вообще говоря, не являются асимптотически наилучшими, Более важным с теоретической точки зрения представляется максимального правдоподобия метод, который приводит к оценкам, при некоторых общих условиях асимптотически наилучшим. Частным случаем последнего является наименьших квадратов метод. Метод Статистические оценки существенно дополняется оцениванием с помощью доверительных границ.
Лит.: Кендалл М., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973; Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
А. В. Прохоров.
| "БСЭ" >> "С" >> "СТ" >> "СТА" >> "СТАТ" |
Статья про "Статистические оценки" в Большой Советской Энциклопедии была прочитана 798 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная