БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ
Навигация:
Библиотека DJVU
БСЭ
 Статистика:

Собственные векторы

Значение слова "Собственные векторы" в Большой Советской Энциклопедии

Собственные векторы линейного преобразования, векторы, которые при этом преобразовании не меняют своего направления, а только умножаются на скаляр. Например, Собственные векторы преобразования, составленного из вращении вокруг некоторой оси и сжатия к перпендикулярной ей плоскости, служат векторы, направленные по этой оси. Координаты х1, х2,..., xn Собственные векторы линейного преобразования n-мерного пространства с матрицей преобразования ||aik|| удовлетворяют системе однородных линейных уравнений 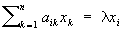, , где l — одно из собственных значений этой матрицы. Если матрица преобразования самосопряжённая (см. Самосопряжённая матрица), то Собственные векторы взаимно перпендикулярны. При самосопряжённом преобразовании сфера переходит в эллипсоид, главными осями которого являются Собственные векторы преобразования.

 

В Большой Советской Энциклопедии рядом со словом "Собственные векторы"

Собственность | Буква "С" | В начало | Буквосочетание "СО" | Собственные движения звёзд


Статья про слово "Собственные векторы" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

  • Florists in america
  • business support in USA
    •