


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Собственные значения
Определение "Собственные значения" в Большой Советской Энциклопедии
Собственные значения линейного преобразования или оператора А, числа l, для которых существует ненулевой вектор х такой, что Ах = lх; вектор х называется собственным вектором. Так, Собственные значения дифференциального оператора L (y) с заданными краевыми условиями служат такие числа l, при которых уравнение L (y) = lу имеет ненулевое решение, удовлетворяющее этим краевым условиям. Например, если оператор L (y) имеет вид у’’, то его Собственные значения при краевых условиях y (0) = у (p) = 0 служат числа вида ln = n2, где n — натуральное число, т.к. уравнению — у’’ = n2у с указанными краевыми условиями удовлетворяют функции уп = sin nx; если же ln ¹ n2 ни при каком натуральном n, то уравнению —у’’ = lу при тех же краевых условиях удовлетворяет только функция у (х) º 0. К изучению Собственные значения линейных операторов приводят многие задачи математики, механики и физики (аналитической геометрии и алгебры, теории колебаний, квантовой механики и т.д.).
Собственные значения матрицы 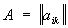 (i, k = 1, 2,..., n) называют Собственные значения соответствующего ей линейного преобразования п-мерного комплексного пространства. Их можно определить также как корни определителя матрицы А — lЕ (где Е — единичная матрица), т. е. корни уравнения
(i, k = 1, 2,..., n) называют Собственные значения соответствующего ей линейного преобразования п-мерного комплексного пространства. Их можно определить также как корни определителя матрицы А — lЕ (где Е — единичная матрица), т. е. корни уравнения , (*)
, (*)
называемого характеристическим уравнением матрицы. Эти числа совпадают для подобных матриц А и В–1 AB (где В — неособенная матрица) и характеризуют поэтому свойства линейного преобразования, не зависящие от выбора системы координат. Каждому корню li; уравнения (*) отвечает вектор xi ¹ 0 (собственный вектор) такой, что Axi = lixi. Если все Собственные значения различны, то множество собственных векторов можно выбрать за базис векторного пространства. В этом базисе линейное преобразование описывается диагональной матрицей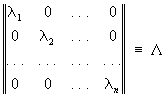 .
.
Каждую матрицу А с различными Собственные значения можно представить в виде С–1LС. Если А — самосопряжённая матрица, то её Собственные значения действительны, собственные векторы ортогональны, а матрицу С можно выбрать унитарной (см. Унитарная матрица). Модуль каждого Собственные значения унитарной матрицы равен 1. Сумма Собственные значения матрицы равна сумме её диагональных элементов, т. е. следу её матрицы. Знание Собственные значения матрицы играет важную роль в исследовании сходимости некоторых приближённых методов решения систем линейных уравнений. См. также Собственные функции.
| "БСЭ" >> "С" >> "СО" >> "СОБ" |
Статья про "Собственные значения" в Большой Советской Энциклопедии была прочитана 838 раз
| Бургер двойного помола |
| Креветки с газировкой |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная