


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Сопряжённые дифференциальные уравнения
Определение "Сопряжённые дифференциальные уравнения" в Большой Советской Энциклопедии
Сопряжённые дифференциальные уравнения, понятие теории дифференциальных уравнений. Уравнением, сопряжённым с дифференциальным уравнением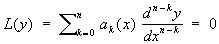 , (1)
, (1)
называется уравнение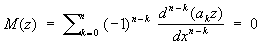 , (2)
, (2)
Соотношение сопряженности взаимно. Для Сопряжённые дифференциальные уравнения имеет место тождество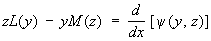 ,
,
где y (у, z) — билинейная форма относительно у, z и их производных до (n - 1)-го порядка включительно. Знание k интегралов сопряжённого уравнения позволяет понизить на k единиц порядок данного уравнения. Если
y1, у2,... уn (3)
— фундаментальная система решений уравнения (1), то фундаментальная система решений уравнения (2) даётся формулами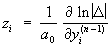
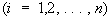 ,
,
где D — определитель Вроньского (см. Вронскиан) системы (3). Если для уравнения (1) заданы краевые условия, то существуют сопряжённые с ними краевые условия для уравнения (2) такие, что уравнения (1) и (2) с соответствующими краевыми условиями определяют сопряжённые дифференциальные операторы (см. Сопряжённые операторы). Понятие сопряженности обобщается также на системы дифференциальных уравнений и на уравнения с частными производными.
| "БСЭ" >> "С" >> "СО" >> "СОП" |
Статья про "Сопряжённые дифференциальные уравнения" в Большой Советской Энциклопедии была прочитана 602 раз
| Коптим скумбрию в коробке |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Объединённая партия гаитянских коммунистов
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная