


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Степень
Определение "Степень" в Большой Советской Энциклопедии
Степень, в первоначальном понимании (целая и положительная Степень) есть произведение нескольких равных сомножителей. Обозначение: 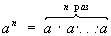 , где а — основание, n — показатель степени, an — степень. Степень a2 называется квадратом, a3 — кубом (a2 — площадь квадрата, a3 — объём куба со стороной а). Основные действия над Степень даются формулами: anam = an+m; an: am = an-m; (an) m = anm. Дальнейшие обобщения Степень: нулевая a0 = 1 (при a ¹ 0); отрицательная a-n = 1/an;
, где а — основание, n — показатель степени, an — степень. Степень a2 называется квадратом, a3 — кубом (a2 — площадь квадрата, a3 — объём куба со стороной а). Основные действия над Степень даются формулами: anam = an+m; an: am = an-m; (an) m = anm. Дальнейшие обобщения Степень: нулевая a0 = 1 (при a ¹ 0); отрицательная a-n = 1/an;
дробная 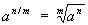 (см. Двучленное уравнение, Извлечение корня) и Степень с иррациональным показателем
(см. Двучленное уравнение, Извлечение корня) и Степень с иррациональным показателем 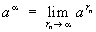 , где rп — произвольная последовательность рациональных чисел, стремящаяся к a.
, где rп — произвольная последовательность рациональных чисел, стремящаяся к a.
Все указанные выше правила действий справедливы и для обобщённых Степень В теории аналитических функций рассматривают также Степень с мнимыми основанием и показателем.
| "БСЭ" >> "С" >> "СТ" >> "СТЕ" >> "СТЕП" |
Статья про "Степень" в Большой Советской Энциклопедии была прочитана 641 раз
| Пицца в сковороде |
| Английский рыбный пирог |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная