


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Тауберовы теоремы
Определение "Тауберовы теоремы" в Большой Советской Энциклопедии
Тауберовы теоремы, теоремы, устанавливающие условия, при которых суммируемость ряда или интеграла некоторым методом влечёт его суммируемость более слабым методом (см. Суммирование расходящихся рядов и интегралов). Одной из первых теорем такого типа была теорема австрийского математика А. Таубера (A. Tauber) (1897): если для числового ряда 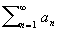 существует предел
существует предел 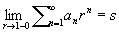 (то есть если он суммируем к s методом Абеля) и если
(то есть если он суммируем к s методом Абеля) и если 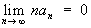 , то этот ряд сходится к s.
, то этот ряд сходится к s.
Тауберовы теоремы применяются при исследованиях во многих областях математики, в частности в аналитической теории чисел и при изучении асимптотического поведения собственных значений и собственных функций дифференциальных операторов.
Лит.: Харди Г., Расходящиеся ряды, пер. с англ., М., 1951.
| "БСЭ" >> "Т" >> "ТА" >> "ТАУ" |
Статья про "Тауберовы теоремы" в Большой Советской Энциклопедии была прочитана 586 раз
| Каша со столетними яйцами |
| Каша со столетними яйцами |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная