


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Собственные функции
Определение "Собственные функции" в Большой Советской Энциклопедии
Собственные функции, понятие математического анализа. При решении многих задач математической физики (в теории колебаний, теплопроводности и т.д.) возникает необходимость в нахождении не равных тождественно нулю решений однородных линейных дифференциальных уравнений L (y) = lу, удовлетворяющих тем или иным краевым условиям. Такие решения называют Собственные функции задачи, а соответствующие значения l — собственными значениями. Если дифференциальное уравнение с соответствующими краевыми условиями самосопряжённое (см. Самосопряжённое дифференциальное уравнение), то его собственные значения действительны, а Собственные функции, соответствующие различным собственным значениям, ортогональны. Если дифференциальное уравнение рассматривается на конечном отрезке и его коэффициенты не имеют на этом отрезке особенностей, то множество Собственные функции счётно (задача имеет дискретный спектр); знание Собственные функции и соответствующих собственных значений позволяет тогда при некоторых условиях получить решение задачи в виде ряда по Собственные функции (см. Фурье метод). Если же уравнение рассматривается на бесконечном промежутке или его коэффициенты имеют особенности (например, если коэффициент при старшей производной обращается в нуль), может существовать континуум Собственные функции, и вместо разложения в ряд получается разложение в интеграл по Собственные функции, аналогичное представлению в виде Фурье интеграла. В этом случае говорят, что задача имеет непрерывный спектр. Многие специальные функции (ортогональные многочлены и др.) служат Собственные функции некоторых уравнений.
В теории интегральных уравнений Собственные функции ядра К (х, у) называют функцию, удовлетворяющую при некотором значении l уравнению .
.
Всякое симметрическое непрерывное ядро имеет Собственные функции В этом случае всякая функция, представимая в виде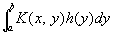 ,
,
может быть разложена в ряд по Собственные функции Если ядро имеет особенности или задано в бесконечной области, то может также возникнуть непрерывный спектр.
Наиболее общим образом Собственные функции можно определить как собственные векторы линейных операторов в линейных функциональных пространствах. В квантовой механике Собственные функции оператора, отвечающего какой-либо физической величине (см. Операторы в квантовой теории), соответствуют состояниям системы, в которых данная физическая величина имеет определённое значение.
Иногда Собственные функции называют также фундаментальными функциями, характеристическими функциями и т.д.
| "БСЭ" >> "С" >> "СО" >> "СОБ" |
Статья про "Собственные функции" в Большой Советской Энциклопедии была прочитана 912 раз
| Бургер двойного помола |
| Шотландский Стовис |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная