


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Тейлора ряд
Определение "Тейлора ряд" в Большой Советской Энциклопедии
Тейлора ряд, степенной ряд вида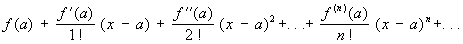 , (1)
, (1)
где f (x) — функция, имеющая при х = а производные всех порядков. Во многих практически важных случаях этот ряд сходится к f (x) на некотором интервале с центром в точке а: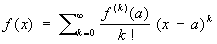 (2)
(2)
(эта формула опубликована в 1715 Б. Тейлором). Разность Rn (x) = f (x) — Sn (x), где Sn (x) — сумма первых n + 1 членов ряда (1), называется остаточным членом Тейлора ряд Формула (2) справедлива, если 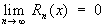 . Тейлора ряд можно представить в виде
. Тейлора ряд можно представить в виде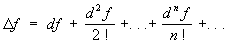 ,
,
применимом и к функциям многих переменных.
При а = 0 разложение функции в Тейлора ряд (исторически неправильно называемый в этом случае рядом Маклорена; см. Маклорена ряд) принимает вид: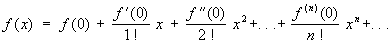 ,
,
в частности: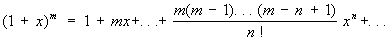 (3)
(3)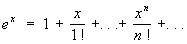 (4)
(4)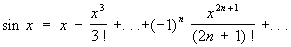 (5)
(5)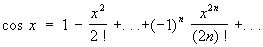 (6)
(6)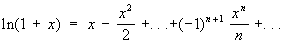 .(7)
.(7)
Ряд (3), являющийся обобщением на случай дробных и отрицательных показателей формулы бинома Ньютона, сходится: при -1< х < 1, если m < -1; при -1< x £ 1, если -1< m < 0; при -1 £ x £ 1, если m > 0. Ряды (4), (5) и (6) сходятся при любых значениях х, ряд (7) сходится при -1< x £ 1.
Функция f (z) комплексного переменного z, регулярная в точке а, раскладывается в Тейлора ряд по степеням z — а внутри круга с центром в точке я и с радиусом, равным расстоянию от а до ближайшей особой точки функции f (z). Вне этого круга Тейлора ряд расходится, поведение же его на границе круга сходимости может быть весьма сложным. Радиус круга сходимости выражается через коэффициенты Тейлора ряд (см. Радиус сходимости).
Тейлора ряд является мощным аппаратом для исследования функций и для приближённых вычислений. См. также Тейлора формула.
Лит.: Хинчин А. Я., Краткий курс математического анализа, М., 1953; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.
| "БСЭ" >> "Т" >> "ТЕ" >> "ТЕЙ" |
Статья про "Тейлора ряд" в Большой Советской Энциклопедии была прочитана 707 раз
| Луковый соус |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная