


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Бесконечно малая
Определение "Бесконечно малая" в Большой Советской Энциклопедии
Бесконечно малая в математике, переменная величина, стремящаяся к пределу, равному нулю. Для того чтобы понятие Бесконечно малая имело точный смысл, необходимо указывать тот процесс изменения, при котором данная величина становится Бесконечно малая Например, величина y = 1/x является Бесконечно малая при аргументе х, стремящемся к бесконечности, а при х, стремящемся к нулю, она оказывается бесконечно большой. Если предел переменной у конечен и равен а, то lim (y - a) = 0 и обратно. Поэтому понятие Бесконечно малая величины можно положить в основу общего определения предела переменной величины. Теория Бесконечно малая является одним из способов построения теории пределов.
При рассмотрении нескольких переменных величин, участвующих в одном и том же процессе изменения, переменные у и z называются эквивалентными, если limz/y = 1; если при этом у является Бесконечно малая, то у и z называются эквивалентными Бесконечно малая Переменная z называется Бесконечно малая относительно у, если z/y есть Бесконечно малая Последний факт часто записывается в виде z = о (у) (читается: «z есть о малое от у»). Если при этом у является Бесконечно малая, то говорят, что z есть Бесконечно малая более высокого порядка, чем у. Часто среди нескольких Бесконечно малая, участвующих в одном и том же процессе изменения, одна из них, скажем у, принимается за главную, и с ней сравниваются все остальные. Тогда говорят, что z есть Бесконечно малая порядка k > 0, если предел lim z/ук существует и отличен от нуля; если же этот предел равен нулю, то z называется Бесконечно малая порядка выше k. Изучение порядков различного рода Бесконечно малая — одна из важных задач математического анализа.
Для случая, когда переменная величина есть функция аргумента х, из общего определения предела вытекает такое развёрнутое определение Бесконечно малая: функция f (x), определённая в окрестности точки x0, называется Бесконечно малая при х, стремящемся к x0, если для любого положительного числа e найдётся такое положительное число d, что для всех x ¹ x0, удовлетворяющих условию |x - x0| < d, выполняется неравенство |f (x)| < e. Этот факт записывается в виде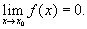
При изучении функции f (x) вблизи точки xo за главную Бесконечно малая принимают приращение независимого переменного Dх = х - х0. Формула
Dy = f’(x0) Dx + о (Dх)
выражает, например, что приращение Dy дифференцируемой функции с точностью до Бесконечно малая порядка выше первого совпадает с её дифференциалом dy = f " (x0) Dx.
Метод Бесконечно малая, или (что то же) метод пределов, является в настоящее время основным методом обоснования математического анализа, почему его и называют также анализом Бесконечно малая Он заменил исчерпывания метод древних и «неделимых» метод. Метод Бесконечно малая был намечен И. Ньютоном (1666) и получил всеобщее признание после работ О. Коши. При помощи Бесконечно малая даются определения таких основных понятий анализа, как сходящийся ряд, интеграл, производная, дифференциал. Кроме того, метод Бесконечно малая служит одним из основных методов приложения математики к задачам естествознания. Это связано с тем, что большинство закономерностей механики и классической физики выражается в виде формул, связывающих Бесконечно малая приращения изучаемых величин, и обращение к Бесконечно малая является обычным приёмом составления дифференциальных уравнений задачи.
Лит. см. при ст. Анализ математический.
С. Б. Стечкин.
| "БСЭ" >> "Б" >> "БЕ" >> "БЕС" |
Статья про "Бесконечно малая" в Большой Советской Энциклопедии была прочитана 774 раз
| Ананасы на гриле |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Звёздная астрономия
- Навигация (морск.)
- Ямполь (пос. гор. типа в Донецкой обл.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс