


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Характер (в математике)
Определение "Характер (в математике)" в Большой Советской Энциклопедии
Характер в математике, функция специального вида, применяемая в чисел теории и теории групп.
В теории чисел Характер (в математике) называют функцию c(n) ¹ 0, определённую для всех целых чисел n и такую, что: 1) c(nm) = c(n)c(m) для всех n и m, 2) существует такое целое число k (период), что c(n + k) = c(n) для всех n. Наименьший из положительных периодов называется основным модулем характера c, а характер с основным модулем k обозначается c(n, k). Примерами Характер (в математике) являются: 1) главный Характер (в математике) по модулю k; c(n, k) = 0, если (n, k) > 1, и c(n, k) = 1, если (n, k) = 1, 2) c(n, k) = 0, если (n, k) > 1, c(n, k) = 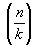 , если (n, k) = 1,
, если (n, k) = 1, 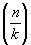 - Якоби символ, k > 1 - нечётное натуральное число. Характер (в математике) степени q по модулю k называется Характер (в математике), равный единице для чисел и, для которых разрешимо сравнение xq º a (modk) (см. Степенной вычет). Такие Характер (в математике) играют важную роль в теории алгебраических чисел. Многие вопросы теории чисел (например, вопрос о распределении простых чисел) связаны с изучением функций L (sc) =
- Якоби символ, k > 1 - нечётное натуральное число. Характер (в математике) степени q по модулю k называется Характер (в математике), равный единице для чисел и, для которых разрешимо сравнение xq º a (modk) (см. Степенной вычет). Такие Характер (в математике) играют важную роль в теории алгебраических чисел. Многие вопросы теории чисел (например, вопрос о распределении простых чисел) связаны с изучением функций L (sc) = 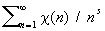 (т. н. L-функций Дирихле). Частным случаем таких функций является дзета-функция x(s), для которой Х (n) º 1.
(т. н. L-функций Дирихле). Частным случаем таких функций является дзета-функция x(s), для которой Х (n) º 1.
Условие периодичности c(n + k) = c(n) позволяет трактовать характеры c(n, k) при фиксированном k > 1 как функции, заданные на приведённой системе вычетов по модулю k, рассматриваемой как группа по умножению, и удовлетворяющие там функциональному уравнению:
c(ab) = c(a) c(b). (1)
Такая трактовка понятия Характер (в математике) позволяет непосредственно перенести его на любую конечную коммутативную группу G. При этом, если n - порядок, e - единица, a - произвольный элемент группы G, то [c(a)] n = c(a n) = c(e) = 1, т. е. c(a) - корень n-й степени из единицы: в частности
|c(a)| º 1. (2)
Характер (в математике) произвольной коммутативной группы G (не обязательно конечной) называют всякую функцию c(а), определённую на G и удовлетворяющую условиям (1) и (2). Если G - топологическая группа, то требуют ещё, чтобы c(а) была непрерывна.
Совокупность всех Характер (в математике) группы G образует группу G1, относительно обыкновенного умножения Характер (в математике) как функций. Если G конечна, то G1 изоморфна G. Для бесконечных групп это уже, вообще говоря, неверно. Например, если G - группа целых чисел, то её Характер (в математике) служат c(n) = einj, где (j - любое действительное число, приведённое по модулю 2p, так что группа Характер (в математике) совпадает с группой вращений окружности. В свою очередь, группа Характер (в математике) для группы вращений окружности совпадает с группой целых чисел [каждый такой Характер (в математике) имеет вид: c(j) = einj]. Эта двойственность была обобщена Л. С. Понтрягиным на широкий класс групп и применена к решению важных проблем топологии (т. н. проблем двойственности для компактов).
Лит.: Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; Чудаков Н. Г., Введение в теорию L-функций Дирихле, М. - Л., 1947; Ленг С., Алгебра, пер. с англ., М., 1968; Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972.
| "БСЭ" >> "Х" >> "ХА" >> "ХАР" >> "ХАРА" |
Статья про "Характер (в математике)" в Большой Советской Энциклопедии была прочитана 566 раз
| Коптим скумбрию в коробке |
| Гороховое пюре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Объединённая партия гаитянских коммунистов
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная