БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ БОЛЬШАЯ СОВЕТСКАЯ ЭНЦИКЛОПЕДИЯ, БСЭ
Навигация:
Библиотека DJVU
БСЭ
 Статистика:

Эйлерова характеристика

Значение слова "Эйлерова характеристика" в Большой Советской Энциклопедии

Эйлерова характеристика многогранника, число ao-a1 +a2, где ao - число вершин, a1 - число рёбер и a2- число граней многогранника. Если многогранник выпуклый или гомеоморфен (см. Гомеоморфизм) выпуклому, то его Эйлерова характеристика равна двум (теорема Л. Эйлера, 1758, известная ещё Р. Декарту).

  Эйлерова характеристика произвольного комплекса есть число 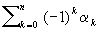, где n - размерность комплекса, ao - число его вершин, a1 - число его рёбер, вообще ak есть число входящих в комплекс k-мерных симплексов. Оказывается, что Эйлерова характеристика равна  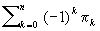(формула Эйлера-Пуанкаре), где pk есть k-мерное число Бетти данного комплекса (см. Топология). Отсюда следует топологическая инвариантность Эйлерова характеристика Ввиду топологической инвариантности Эйлерова характеристика говорят об Эйлерова характеристика поверхности, а также полиэдра, подразумевая под этим Эйлерова характеристика любой триангуляции этой поверхности (этого полиэдра).

 

  Лит.: Александров П. С., Комбинаторная топология, М.- Л., 1947; Понтрягин Л. С., Основы комбинаторной топологии. 2 изд., М., 1976.

 

В Большой Советской Энциклопедии рядом со словом "Эйлерова характеристика"

Эйлера-Фурье формулы | Буква "Э" | В начало | Буквосочетание "ЭЙ" | Эйлеровы интегралы


Статья про слово "Эйлерова характеристика" в Большой Советской Энциклопедии была прочитана 0 раз

Интересное

  • Florists in america
  • business support in USA
    •