


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Топология
Определение "Топология" в Большой Советской Энциклопедии
Топология (от греч. tоpos — место и ¼логия) — часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных подходов к её изучению привели к распадению единой Топология на ряд отделов («общая Топология», «алгебраическая Топология» и др.), отличающихся друг от друга по предмету и методу изучения и фактически весьма мало между собой связанных.
I. Общая топология
Часть Топология, ориентированная на аксиоматическое изучение непрерывности, называется общей Топология Наряду с алгеброй общая Топология составляет основу современного теоретико-множественного метода в математике.
Аксиоматически непрерывность можно определить многими (вообще говоря, неравносильными) способами. Общепринята аксиоматика, основывающаяся на понятии открытого множества. Топологической структурой, или топологией, на множестве Х называют такое семейство его подмножеств, называемых открытыми множествами, что: 1) пустое множество Æ и всё Х открыты; 2) объединение любого числа и пересечение конечного числа открытых множеств открыто. Множество, на котором задана топологическая структура, называют топологическим пространством. В топологическом пространстве Х можно определить все основные понятия элементарного анализа, связанные с непрерывностью. Например, окрестностью точки x Î X называют произвольное открытое множество, содержащее эту точку; множество A Ì X называют замкнутым, если его дополнение Х А открыто; замыканием множества А называют наименьшее замкнутое множество, содержащее A; если это замыкание совпадает с X, то А называют всюду плотным в Х и т.д.
По определению, Æ и Х являются одновременно замкнутыми и открытыми множествами. Если в Х нет других множеств, одновременно замкнутых и открытых, то топологическое пространство Х называют связным. Наглядно связное пространство состоит из одного «куска», а несвязное — из нескольких.
Любое подмножество А топологического пространства Х обладает естественной топологической структурой, состоящей из пересечений с А открытых множеств из X. Снабженное этой структурой А называют подпространством пространства X. Каждое метрическое пространство становится топологическим, если за его открытые множества принять множества, содержащие вместе с произвольной точкой некоторую её e-окрестность (шар радиуса e с центром в этой точке). В частности, любое подмножество n-мерного евклидова пространства 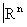 является топологическим пространством. Теория таких пространств (под названием «геометрической Топология») и теория метрических пространств включаются по традиции в общую Топология
является топологическим пространством. Теория таких пространств (под названием «геометрической Топология») и теория метрических пространств включаются по традиции в общую Топология
Геометрическая Топология довольно четко распадается на две части: изучение подмножеств 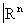 произвольной сложности, подчинённых тем или иным ограничениям общего характера (примером является так называемая теория континуумов, то есть связных ограниченных замкнутых множеств), и изучение способов, какими в
произвольной сложности, подчинённых тем или иным ограничениям общего характера (примером является так называемая теория континуумов, то есть связных ограниченных замкнутых множеств), и изучение способов, какими в 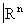 могут быть вложены такие простые топологические пространства, как сфера, шар и т.п. (вложения в
могут быть вложены такие простые топологические пространства, как сфера, шар и т.п. (вложения в 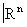 , например, сфер могут быть очень сложно устроенными).
, например, сфер могут быть очень сложно устроенными).
Открытым покрытием топологического пространства Х называют семейство его открытых множеств, объединением которого является всё X. Топологическое пространство Х называют компактным (в другой терминологии —бикомпактным), если любое его открытое покрытие содержит конечное число элементов, также образующих покрытие. Классическая теорема Гейне — Бореля утверждает, что любое ограниченное замкнутое подмножество 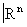 компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Топология, имеющих общематематическое значение.
компактно. Оказывается, что все основные теоремы элементарного анализа об ограниченных замкнутых множествах (например, теорема Вейерштрасса о том, что на таком множестве непрерывная функция достигает своего наибольшего значения) справедливы для любых компактных топологических пространств. Это определяет фундаментальную роль, которую играют компактные пространства в современной математике (особенно в связи с теоремами существования). Выделение класса компактных топологических пространств явилось одним из крупнейших достижений обшей Топология, имеющих общематематическое значение.
Открытое покрытие {Vb} называют вписанным в покрытие {Ua}, если для любого b существует a такое, что Vb Ì Ua. Покрытие {Vb} называют локально конечным, если каждая точка х Î Х обладает окрестностью, пересекающейся только с конечным числом элементов этого покрытия. Топологическое пространство называют паракомпактным, если в любое его открытое покрытие можно вписать локально конечное покрытие. Класс паракомпактных пространств является примером классов топологических пространств, получающихся наложением так называемых условий типа компактности. Этот класс очень широк, в частности он содержит все метризуемые топологические пространства, то есть пространства X, в которых можно ввести такую метрику r, что Топология, порожденная r в X, совпадает с Топология, заданной в X.
Кратностью открытого покрытия называют наибольшее число k такое, что найдётся k его элементов, имеющих непустое пересечение. Наименьшее число n, обладающее тем свойством, что в любое конечное открытое покрытие топологического пространства Х можно вписать открытое покрытие кратности £n + 1, обозначается символом dimХ и называется размерностью X. Это название оправдано тем, что в элементарно-геометрических ситуациях dimХ совпадает с обычно понимаемой размерностью, например dim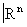 = n. Возможны и др. числовые функции топологического пространства X, отличающиеся от dimX, но в простейших случаях совпадающие с dimX. Их изучение составляет предмет общей теории размерности — наиболее геометрически ориентированной части общей Топология Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п.
= n. Возможны и др. числовые функции топологического пространства X, отличающиеся от dimX, но в простейших случаях совпадающие с dimX. Их изучение составляет предмет общей теории размерности — наиболее геометрически ориентированной части общей Топология Только в рамках этой теории удаётся, например, дать чёткое и достаточно общее определение интуитивного понятия геометрической фигуры и, в частности, понятия линии, поверхности и т.п.
Важные классы топологических пространств получаются наложением так называемых аксиом отделимости. Примером является так называемая аксиома Хаусдорфа, или аксиома T2, требующая, чтобы любые две различные точки обладали непересекающимися окрестностями. Топологическое пространство, удовлетворяющее этой аксиоме, называется хаусдорфовым, или отделимым. Некоторое время в математической практике встречались почти исключительно хаусдорфовы пространства (например, любое метрическое пространство хаусдорфово). Однако роль нехаусдорфовых топологических пространств в анализе и геометрии постоянно растет.
Топологические пространства, являющиеся подпространствами хаусдорфовых (би) компактных пространств, называются вполне регулярными или тихоновскими. Их тоже можно охарактеризовать некоторой аксиомой отделимости, а именно: аксиомой, требующей, чтобы для любой точки x0 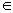 Х и любого не содержащего её замкнутого множества F
Х и любого не содержащего её замкнутого множества F 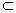 Х существовала непрерывная функция g : Х ® [0, 1], равная нулю в x0 и единице на F.
Х существовала непрерывная функция g : Х ® [0, 1], равная нулю в x0 и единице на F.
Топологические пространства, являющиеся открытыми подпространствами хаусдорфовых компактных, называются локально компактными пространствами. Они характеризуются (в классе хаусдорфовых пространств) тем, что каждая их точка обладает окрестностью с компактным замыканием (пример: евклидово пространство). Любое такое пространство дополняется одной точкой до компактного (пример: присоединением одной точки из плоскости получается сфера комплексного переменного, а из 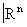 — сфера S n).
— сфера S n).
Отображение f : X ® Y топологическое пространства Х в топологическое пространство Y называют непрерывным отображением, если для любого открытого множества V Ì Y множество f—1(V) открыто в X. Непрерывное отображение называют гомеоморфизмом, если оно взаимно однозначно и обратное отображение f—1: Y ® X непрерывно. Такое отображение устанавливает взаимно однозначное соответствие между открытыми множествами топологических пространств Х и Y, перестановочное с операциями объединения и пересечения множеств. Поэтому все топологические свойства (то есть свойства, формулируемые в терминах открытых множеств) этих пространств одни и те же, и с топологической точки зрения гомеоморфные топологические пространства (то есть пространства, для которых существует хотя бы один гомеоморфизм Х ® Y) следует считать одинаковыми (подобно тому как в евклидовой геометрии одинаковыми считаются фигуры, которые можно совместить движением). Например, гомеоморфны («топологически одинаковы») окружность и граница квадрата, шестиугольника и т.п. Вообще любые две простые (не имеющие двойных точек) замкнутые линии гомеоморфны. Напротив, окружность не гомеоморфна прямой (ибо удаление точки не нарушает связности окружности, но нарушает связность прямой; по той же причине прямая не гомеоморфна плоскости, а окружность не гомеоморфна «восьмёрке»). Окружность не гомеоморфна также и плоскости (выкиньте не одну, а две точки).
Пусть {Хa} — произвольное семейство топологических пространств. Рассмотрим множество Х всех семейств вида {хa}, где xa 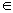 Xa (прямое произведение множеств Xa). Для любого a формула
Xa (прямое произведение множеств Xa). Для любого a формула 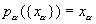 определяет некоторое отображение
определяет некоторое отображение 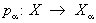 (называется проекцией). Вообще говоря, в Х можно ввести много топологических структур, относительно которых все отображения pa непрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество Х называется топологическим произведением топологических пространств Хa и обозначается символом ПХa (а в случае конечного числа сомножителей — символом X1 ´ ... ´ Xn). В явном виде открытые множества пространства Х можно описать как объединения конечных пересечений всех множеств вида
(называется проекцией). Вообще говоря, в Х можно ввести много топологических структур, относительно которых все отображения pa непрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество Х называется топологическим произведением топологических пространств Хa и обозначается символом ПХa (а в случае конечного числа сомножителей — символом X1 ´ ... ´ Xn). В явном виде открытые множества пространства Х можно описать как объединения конечных пересечений всех множеств вида 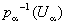 , где Ua открыто в Xa. Топологическое пространство Х обладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений fa : Y ® Xa существует единственное непрерывное отображение f : Y ® X, для которого
, где Ua открыто в Xa. Топологическое пространство Х обладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений fa : Y ® Xa существует единственное непрерывное отображение f : Y ® X, для которого 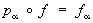 при всех a. Пространство
при всех a. Пространство 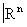 является топологическим произведением n экземпляров числовой прямой. Одной из важнейших теорем общей Топология является утверждение о том, что топологическое произведение компактных топологических пространств компактно.
является топологическим произведением n экземпляров числовой прямой. Одной из важнейших теорем общей Топология является утверждение о том, что топологическое произведение компактных топологических пространств компактно.
Если Х — топологическое пространство, а Y — произвольное множество и если задано отображение p : X ® Y пространства Х на множество Y (например, если Y является фактормножеством Х по некоторому отношению эквивалентности, а p представляет собой естественную проекцию, сопоставляющую с каждым элементом х Î Х его класс эквивалентности), то можно ставить вопрос о введении в Y топологической структуры, относительно которой отображение p непрерывно. Наиболее «богатую» (открытыми множествами) такую структуру получают, полагая открытыми множествами в Y все те множества V Ì Y, для которых множество f‑1(V) Ì Х открыто в X. Снабженное этой топологической структурой множество Y называется факторпространством топологического пространства Х (по отношению к p ). Оно обладает тем свойством, что произвольное отображение f : Y ® Z тогда и только тогда непрерывно, когда непрерывно отображение 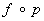 : X ® Z. Непрерывное отображение p : X ® Y называется факторным, если топологическое пространство Y является по отношению к p факторпространством топологического пространства X. Непрерывное отображение p : X ® Y называется открытым, если для любого открытого множества U Ì Х множество p(U) открыто в Y, и замкнутым, если для любого замкнутого множества F Ì Х множество p(F) замкнуто в Y. Как открытые, так и замкнутые непрерывные отображения f : Х ® Y, для которых f(X) = Y, являются факторными.
: X ® Z. Непрерывное отображение p : X ® Y называется факторным, если топологическое пространство Y является по отношению к p факторпространством топологического пространства X. Непрерывное отображение p : X ® Y называется открытым, если для любого открытого множества U Ì Х множество p(U) открыто в Y, и замкнутым, если для любого замкнутого множества F Ì Х множество p(F) замкнуто в Y. Как открытые, так и замкнутые непрерывные отображения f : Х ® Y, для которых f(X) = Y, являются факторными.
Пусть Х — топологическое пространство, А — его подпространство и f : A ® Y — непрерывное отображение. Предполагая топологические пространства Х и Y непересекающимися, введём в их объединении Х È Y топологическую структуру, считая открытыми множествами объединения открытых множеств из Х и Y. Далее, введём в пространстве Х È Y наименьшее отношение эквивалентности, в котором a ~ f(a) для любой точки a Î А. Соответствующее факторпространство обозначается символом X È fY, и о нём говорят, что оно получено приклеиванием топологического пространства Х к топологическому пространству Y по А посредством непрерывного отображения f. Эта простая и наглядная операция оказывается очень важной, так как позволяет получать из сравнительно простых топологических пространств более сложные. Если Y состоит из одной точки, то пространство Х È fY обозначается символом Х/А и о нём говорят, что оно получено из Х стягиванием А в точку. Например, если Х — диск, а А — его граничная окружность, то Х/А гомеоморфно сфере.
2. Равномерная топология
Часть Топология, изучающая аксиоматическое понятие равномерной непрерывности, называется равномерной Топология Известное из анализа определение равномерной непрерывности числовых функций непосредственно переносится на отображения любых метрических пространств. Поэтому аксиоматику равномерной непрерывности обычно получают, отталкиваясь от метрических пространств. Подробно исследованы два аксиоматических подхода к равномерной непрерывности, основанных соответственно на понятиях близости и окружения диагонали.
Подмножества А и В метрических пространства Х называются близкими (обозначение AdB ), если для любого e > 0 существуют точки a Î А и b Î В, расстояние между которыми < e. Принимая основные свойства этого отношения за аксиомы, приходят к следующему определению: (отделимой) структурой близости на множестве Х называется такое отношение d на множестве всех его подмножеств, что: 1) Æ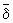 X (символом
X (символом 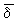 обозначается отрицание отношения d; 2) A
обозначается отрицание отношения d; 2) A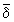 B1 и A
B1 и A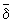 B2 Û A
B2 Û A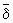 (B1 U B2 ); 3) {x}
(B1 U B2 ); 3) {x}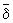 {y} Û x ¹ y; 4) если А
{y} Û x ¹ y; 4) если А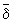 В, то существует такое множество С
В, то существует такое множество С 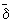 В, что А
В, что А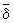 (Х С). Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости Х в пространство близости Y называется близостно непрерывным, если образы близких в Х множеств близки в Y. Пространства близости Х и Y называются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение X ® Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Топология эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество u Ì x открытым, если {x}
(Х С). Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости Х в пространство близости Y называется близостно непрерывным, если образы близких в Х множеств близки в Y. Пространства близости Х и Y называются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение X ® Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Топология эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество u Ì x открытым, если {x}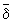 (X U) для любой точки х Î U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства Х все структуры близости на X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии — би-компактными расширениями) вХ — компактными хаусдорфовыми топологическими пространствами, содержащими Х в качестве всюду плотного пространства. Структура близости d, соответствующая расширению вХ, характеризуется тем, что АdВ тогда и только тогда, когда замыкания множеств А и В пересекаются в bX. В частности, на любом компактном хаусдорфовом топологическом пространстве Х существует единственная структура близости, порождающая его топологическую структуру.
(X U) для любой точки х Î U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства Х все структуры близости на X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии — би-компактными расширениями) вХ — компактными хаусдорфовыми топологическими пространствами, содержащими Х в качестве всюду плотного пространства. Структура близости d, соответствующая расширению вХ, характеризуется тем, что АdВ тогда и только тогда, когда замыкания множеств А и В пересекаются в bX. В частности, на любом компактном хаусдорфовом топологическом пространстве Х существует единственная структура близости, порождающая его топологическую структуру.
Другой подход основан на том, что равномерную непрерывность в метрическом пространстве Х можно определить в терминах отношения «точки х и у находятся на расстоянии, не большем e». С общей точки зрения, отношение на Х есть не что иное как произвольное подмножество U прямого произведения Х ´ X. Отношение «тождество» является с этой точки зрения диагональю D Ì Х ´ X, то есть множеством точек вида (х, х), х Î X. Для любого отношения U определено обратное отношение U—1 = {(х, у); (у, х) Î U } и для любых двух отношений U и V определена их композиция U × V = {(х, у); существует z Î Х такое, что (х, z) Î U, (z, y) Î V }. Семейство отношений {U } называется (отделимой) равномерной структурой на Х (а отношения U называется окружениями диагонали), если: 1) пересечение любых двух окружений диагонали содержит окружение диагонали; 2) каждое окружение диагонали содержит D, и пересечение всех окружений диагонали совпадает с D; 3) вместе с U окружением диагонали является и U—1; 4) для любого окружения диагонали U существует такое окружение диагонали W, что W o W Ì U. Множество, наделённое равномерной структурой, называется равномерным пространством. Отображение f : X ® Y равномерного пространства Х в равномерное пространство Y называется равномерно непрерывным, если прообраз при отображении f ´ f : Х ´ Х ® Y ´ Y любого окружения диагонали V Ì Y ´ Y содержит некоторое окружение диагонали из Х ´ X. Равномерные пространства Х и Y называются равномерно гомеоморфными, если существует взаимно однозначное равномерно непрерывное отображение Х ® Y, обратное к которому также является равномерно непрерывным отображением.
В равномерной Топология такие равномерные пространства считаются одинаковыми. Каждая равномерная структура на Х определяет некоторую структуру близости: АdВ тогда и только тогда, когда (A ´ В ) Ç U ¹ Æ для любого окружения диагонали U Ì X ´ X. При этом равномерно непрерывные отображения оказываются близостно непрерывными.
3. Алгебраическая топология
Пусть каждому топологическому пространству Х (из некоторого класса) поставлен в соответствие некоторый алгебраический объект h(X) (группа, кольцо и т.п.), а каждому непрерывному отображению f : X ® Y — некоторый гомоморфизм h(f) : h(X) ® h(Y) (или h(f) : h(Y) ® h(X), являющийся тождественным гомоморфизмом, когда f представляет собой тождественное отображение. Если h(f1 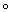 f2) = h(f1)
f2) = h(f1) 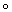 h(f2) (или, соответственно, h(f1
h(f2) (или, соответственно, h(f1 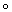 f2) = h(f2)
f2) = h(f2) 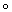 h(f1), то говорят, что h представляет собой функтор (соответственно кофунктор). Большинство задач алгебраической Топология так или иначе связано со следующей задачей распространения: для данного непрерывного отображения f : A ® Y подпространства A Ì Х в некоторое топологическое пространство Y найти непрерывное отображение g : X ® Y, совпадающее на A с f, то есть такое, что f = g×i, где i : А ® Х — отображение вложения (i(a) = а для любой точки а Î A). Если такое непрерывное отображение g существует, то для любого функтора (кофунктора) h существует такой гомоморфизм (j: h(X) ® h(Y) (гомоморфизм j: h(Y) ® h(X)), что h(f) = j
h(f1), то говорят, что h представляет собой функтор (соответственно кофунктор). Большинство задач алгебраической Топология так или иначе связано со следующей задачей распространения: для данного непрерывного отображения f : A ® Y подпространства A Ì Х в некоторое топологическое пространство Y найти непрерывное отображение g : X ® Y, совпадающее на A с f, то есть такое, что f = g×i, где i : А ® Х — отображение вложения (i(a) = а для любой точки а Î A). Если такое непрерывное отображение g существует, то для любого функтора (кофунктора) h существует такой гомоморфизм (j: h(X) ® h(Y) (гомоморфизм j: h(Y) ® h(X)), что h(f) = j 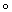 h(i) (соответственно h(f) = h(i)
h(i) (соответственно h(f) = h(i) 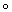 j); им будет гомоморфизм j = h(g). Следовательно, несуществование гомоморфизма j (хотя бы для одного функтора h) влечёт несуществование отображения g. К этому простому принципу могут быть фактически сведены почти все методы алгебраических Топология Например, существует функтор h, значение которого на шаре E n является тривиальной, а на ограничивающей шар сфере S n—1 — нетривиальной группой. Уже отсюда следует отсутствие так называемой ретракции — непрерывного отображения р : E n ® S n—1, неподвижного на S n—1, то есть такого, что композиция р×i, где i : S n‑1 ® E n — отображение вложения, представляет собой тождественное отображение (если р существует, то тождественное отображение группы h(S n—1) будет композицией отображений h(i) : h(S n—1) ® h(E n) и h(p) : h(E n) ® h(S n—1), что при тривиальной группе h(E n) невозможно). Однако этот, по существу, элементарно-геометрический и (при n = 2) наглядно очевидный факт (физически означающий возможность натянуть на круглый обруч барабан) до сих пор не удалось доказать без привлечения алгебраико-топологических методов. Его непосредственным следствием является утверждение, что любое непрерывное отображение f : E n ® E n имеет хотя бы одну неподвижную точку, то есть уравнение f(x) = х имеет в E n хотя бы одно решение (если f(x) ¹ x для всех х Î E n, то, приняв за р(х) точку из S n—1, коллинеарную точкам f(x) и х и такую, что отрезок с концами f(x) и р(х) содержит х, получим ретракцию р : E n ® S n—1). Эта теорема о неподвижной точке была одной из первых теорем алгебраической Топология, а затем явилась источником целой серии разнообразных теорем существования решений уравнений.
j); им будет гомоморфизм j = h(g). Следовательно, несуществование гомоморфизма j (хотя бы для одного функтора h) влечёт несуществование отображения g. К этому простому принципу могут быть фактически сведены почти все методы алгебраических Топология Например, существует функтор h, значение которого на шаре E n является тривиальной, а на ограничивающей шар сфере S n—1 — нетривиальной группой. Уже отсюда следует отсутствие так называемой ретракции — непрерывного отображения р : E n ® S n—1, неподвижного на S n—1, то есть такого, что композиция р×i, где i : S n‑1 ® E n — отображение вложения, представляет собой тождественное отображение (если р существует, то тождественное отображение группы h(S n—1) будет композицией отображений h(i) : h(S n—1) ® h(E n) и h(p) : h(E n) ® h(S n—1), что при тривиальной группе h(E n) невозможно). Однако этот, по существу, элементарно-геометрический и (при n = 2) наглядно очевидный факт (физически означающий возможность натянуть на круглый обруч барабан) до сих пор не удалось доказать без привлечения алгебраико-топологических методов. Его непосредственным следствием является утверждение, что любое непрерывное отображение f : E n ® E n имеет хотя бы одну неподвижную точку, то есть уравнение f(x) = х имеет в E n хотя бы одно решение (если f(x) ¹ x для всех х Î E n, то, приняв за р(х) точку из S n—1, коллинеарную точкам f(x) и х и такую, что отрезок с концами f(x) и р(х) содержит х, получим ретракцию р : E n ® S n—1). Эта теорема о неподвижной точке была одной из первых теорем алгебраической Топология, а затем явилась источником целой серии разнообразных теорем существования решений уравнений.
Вообще говоря, установление несуществования гомоморфизма (j тем легче, чем сложнее алгебраическая структура объектов h(X). Поэтому в алгебраических Топология рассматриваются алгебраические объекты чрезвычайно сложной природы, и требования алгебраической топологии существенно стимулировали развитие абстрактной алгебры.
Топологическое пространство Х называется клеточным пространством, а также клеточным разбиением (или CW-комплексом), если в нём указана возрастающая последовательность подпространств X 0 Ì ¼ Ì X n—1 Ì X n Ì ¼ (называется остовами клеточного пространства X), объединением которых является всё X, причём выполнены следующие условия: 1) множество U Ì X тогда и только тогда открыто в X, когда для любого n множество U Ç X n открыто в X n; 2) X n получается из X n—1 приклеиванием некоторого семейства n-мepных шаров по их граничным (n—1)-мepным сферам (посредством произвольного непрерывного отображения этих сфер в X n—1); 3) X0 состоит из изолированных точек. Таким образом, структура клеточного пространства состоит, грубо говоря, в том, что оно представлено в виде объединения множеств, гомеоморфных открытым шарам (эти множества называются клетками). В алгебраических Топология изучаются почти исключительно клеточные пространства, поскольку специфика задач алгебраических Топология для них уже полностью проявляется. Более того, фактически для алгебраических Топология интересны некоторые особо простые клеточные пространства (типа полиэдров, см. ниже), но сужение класса клеточных пространств, как правило, существенно осложняет исследование (поскольку многие полезные операции над клеточными пространствами выводят из класса полиэдров).
Два непрерывных отображения f, g : X ® Y называются гомотопными, если они могут быть непрерывно продеформированы друг в друга, то есть если существует такое семейство непрерывных отображений ft : X ® Y, непрерывно зависящих от параметра t Î [0, 1], что f0 = f и f1 = g (непрерывная зависимость от t означает, что формула F(x, t) = ft(x), х Î X, t Î [0, 1] определяет непрерывное отображение F : Х ´ [0, 1] ® Y; это отображение, а также семейство {ft } называют гомотопией, связывающей f с g). Совокупность всех непрерывных отображений X ® Y распадается на гомотопические классы гомотопных между собой отображений. Множество гомотопических классов непрерывных отображений из Х в Y обозначается символом [X, Y]. Изучение свойств отношения гомотопности и, в частности, множеств [X, Y] составляет предмет так называемой гомотопической топологии (или теории гомотопий). Для большинства интересных топологических пространств множества [X, Y] конечны или счётны и могут быть в явном виде эффективно вычислены. Топологические пространства Х и Y называются гомотопически эквивалентными, или имеющими один и тот же гомотопический тип, если существуют такие непрерывные отображения f : Х ® Y и g : Y ® Х, что непрерывные отображения g×f : Х ® Х и f×g : Y ® Y гомотопны соответствующим тождественным отображениям. В гомотопической Топология такие пространства следует рассматривать как одинаковые (все их «гомотопические инварианты» совпадают).
Оказывается, что во многих случаях (в частности, для клеточных пространств) разрешимость задачи распространения зависит только от гомотопического класса непрерывного отображения f : A ® Y; точнее, если для f распространение g : Х ® Y существует, то для любой гомотопии ft : A ® Y (с f0 = f) существует распространение gt : Х ® Y такое, что g0 = g. Поэтому вместо f можно рассматривать его гомотопический класс [f] и в соответствии с этим изучать лишь гомотопически инвариантные функторы (кофункторы) h, то есть такие, что h(f0) = h(f1), если отображения f0 и f1 гомотопны. Это приводит к настолько тесному переплетению алгебраической и гомотопической Топология, что их можно рассматривать как единую дисциплину.
Для любого топологического пространства Y формулы h(X) = [X, Y] и h(f) = [j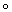 f], где f : X1 ® X2 и j : X2 ® Y, определяют некоторый гомотопически инвариантный кофунктор h, о котором говорят, что он представлен топологическим пространством Y. Это — стандартный (и по существу единственный) приём построения гомотопических инвариантных кофункторов. Чтобы множество h(X) оказалось, скажем, группой, нужно У выбрать соответствующим образом, например потребовать, чтобы оно было топологической группой (вообще говоря, это не совсем так: необходимо выбрать в Х некоторую точку x0 и рассматривать лишь непрерывные отображения и гомотопии, переводящие x0 в единицу группы; это техническое усложнение будет, однако, в дальнейшем игнорироваться). Более того, достаточно, чтобы Y было топологической группой «в гомотопическом смысле», то есть чтобы аксиомы ассоциативности и существования обратного элемента (утверждающие фактически совпадение некоторых отображений) выполнялись бы только «с точностью до гомотопии». Такие топологические пространства называются Н-пространствами. Таким образом, каждое Н-пространство Y задаёт гомотопически инвариантный кофунктор h(X) = [X, Y], значениями которого являются группы.
f], где f : X1 ® X2 и j : X2 ® Y, определяют некоторый гомотопически инвариантный кофунктор h, о котором говорят, что он представлен топологическим пространством Y. Это — стандартный (и по существу единственный) приём построения гомотопических инвариантных кофункторов. Чтобы множество h(X) оказалось, скажем, группой, нужно У выбрать соответствующим образом, например потребовать, чтобы оно было топологической группой (вообще говоря, это не совсем так: необходимо выбрать в Х некоторую точку x0 и рассматривать лишь непрерывные отображения и гомотопии, переводящие x0 в единицу группы; это техническое усложнение будет, однако, в дальнейшем игнорироваться). Более того, достаточно, чтобы Y было топологической группой «в гомотопическом смысле», то есть чтобы аксиомы ассоциативности и существования обратного элемента (утверждающие фактически совпадение некоторых отображений) выполнялись бы только «с точностью до гомотопии». Такие топологические пространства называются Н-пространствами. Таким образом, каждое Н-пространство Y задаёт гомотопически инвариантный кофунктор h(X) = [X, Y], значениями которого являются группы.
Аналогичным («двойственным») образом, каждое топологическое пространство Y задаёт по формулам h(X) = [Y, X], h(f) = [f 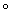 j], где f : X1 ® X2 и j : Y ® X1, некоторый функтор h. Чтобы h(X) было группой, нужно, чтобы Y обладало определённой алгебраической структурой, в некотором точно определённом смысле двойственной структуре Н-пространства. Топологические пространства, наделённые этой структурой, называются ко-Н-пространствами. Примером ко-Н-пространства является n-мepная сфера S n (при n ³ 1). Таким образом, для любого топологического пространства Х формула pnX = [S n, X] определяет некоторую группу pnX, n ³ 1, которая называется n-й гомотопической группой пространства X. При n = 1 она совпадает с фундаментальной группой. При n > 1 группа pnX коммутативна. Если p1X = {1}, то Х называется односвязным.
j], где f : X1 ® X2 и j : Y ® X1, некоторый функтор h. Чтобы h(X) было группой, нужно, чтобы Y обладало определённой алгебраической структурой, в некотором точно определённом смысле двойственной структуре Н-пространства. Топологические пространства, наделённые этой структурой, называются ко-Н-пространствами. Примером ко-Н-пространства является n-мepная сфера S n (при n ³ 1). Таким образом, для любого топологического пространства Х формула pnX = [S n, X] определяет некоторую группу pnX, n ³ 1, которая называется n-й гомотопической группой пространства X. При n = 1 она совпадает с фундаментальной группой. При n > 1 группа pnX коммутативна. Если p1X = {1}, то Х называется односвязным.
Клеточное пространство Х называется пространством K(G, n), если pi(X) = 0 при i ¹ n и pnX = G; такое клеточное пространство существует для любого n ³ 1 и любой группы G (коммутативной при n > 1) и с точностью до гомотопической эквивалентности определено однозначно. При n > 1 (а также при n = 1, если группа G коммутативна) пространство K(G, n) оказывается Н-пространством и потому представляет некоторую группу H n(X; G) = [X; K(G, n)]. Эта группа называется n-мepной группой когомологий топологического пространства Х с группой коэффициентов G. Она является типичным представителем целого ряда важных кофункторов, к числу которых принадлежит, например, К-функтор KO(X) = [Х, BO], представляемый так называемым бесконечномерным грассманианом BO, группы ориентированных кобордизмов WnX и т.п.
Если G является кольцом, то прямая сумма Н*(Х; G) групп H n(X; G) является алгеброй над G. Более того, эта прямая сумма обладает очень сложной алгебраической структурой, в которую (при G = Zp, где Zp — циклическая группа порядка р) входит действие на Н*(Х; G) некоторой некоммутативной алгебры 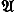 p, называемой алгеброй Стинрода. Сложность этой структуры позволяет, с одной стороны, выработать эффективные (но совсем не простые) методы вычисления групп H n(X; G), а с другой — установить связи между группами H n(X; G) и другими гомотопически инвариантными функторами (например, гомотопическими группами pnX), позволяющие часто в явном виде вычислить и эти функторы.
p, называемой алгеброй Стинрода. Сложность этой структуры позволяет, с одной стороны, выработать эффективные (но совсем не простые) методы вычисления групп H n(X; G), а с другой — установить связи между группами H n(X; G) и другими гомотопически инвариантными функторами (например, гомотопическими группами pnX), позволяющие часто в явном виде вычислить и эти функторы.
Исторически группам когомологий предшествовали так называемые группы гомологий Hn(X; G), являющиеся гомотопическими группами pnM(X, G) некоторого клеточного пространства M(X, G), однозначно строящегося по клеточному пространству Х и группе G. Группы гомологий и когомологий в определённом смысле двойственны друг другу, и их теории по существу равносильны. Однако алгебраическая структура, имеющаяся в группах гомологий, менее привычна (например, эти группы составляют не алгебру, а так называемую коалгебру), и поэтому в вычислениях обычно пользуются группами когомологий. Вместе с тем в некоторых вопросах группы гомологий оказываются более удобными, поэтому они также изучаются. Часть алгебраических Топология, занимающаяся изучением (и применением) групп гомологий и когомологий, называется теорией гомологий.
Перенесение результатов алгебраических Топология на пространства более общие, чем клеточные пространства, составляет предмет так называемой общей алгебраической Топология В частности, общая теория гомологий изучает группы гомологий и когомологий произвольных топологических пространств и их применения. Оказывается, что вне класса компактных клеточных пространств различные подходы к построению этих групп приводят, вообще говоря, к различным результатам, так что для неклеточных топологических пространств возникает целый ряд различных групп гомологий и когомологий. Основное применение общая теория гомологий находит в теории размерности и в теории так называемых законов двойственности (описывающих взаимоотношения между топологическими свойствами двух дополнительных подмножеств топологического пространства), и её развитие было во многом стимулировано нуждами этих теорий.
4. Кусочно-линейная топология
Подмножество Р Î 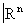 называется конусом с вершиной а и основанием В, если каждая его точка принадлежит единственному отрезку вида ab, где b Î В. Подмножество Х Î
называется конусом с вершиной а и основанием В, если каждая его точка принадлежит единственному отрезку вида ab, где b Î В. Подмножество Х Î 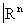 называется полиэдром, если любая его точка обладает в Х окрестностью, замыкание которой является конусом с компактным основанием. Непрерывное отображение f : X ® Y полиэдров называется кусочно-линейным, если оно линейно на лучах каждой конической окрестности любой точки х Î X. Взаимно однозначное кусочно-линейное отображение, обратное к которому также кусочно-линейно, называется кусочно-линейным изоморфизмом. Предметом кусочно-линейной Топология является изучение полиэдров и их кусочно-линейных отображений. В кусочно-линейной Топология полиэдры считаются одинаковыми, если они кусочно-линейно изоморфны.
называется полиэдром, если любая его точка обладает в Х окрестностью, замыкание которой является конусом с компактным основанием. Непрерывное отображение f : X ® Y полиэдров называется кусочно-линейным, если оно линейно на лучах каждой конической окрестности любой точки х Î X. Взаимно однозначное кусочно-линейное отображение, обратное к которому также кусочно-линейно, называется кусочно-линейным изоморфизмом. Предметом кусочно-линейной Топология является изучение полиэдров и их кусочно-линейных отображений. В кусочно-линейной Топология полиэдры считаются одинаковыми, если они кусочно-линейно изоморфны.
Подмножество Х Î 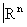 тогда и только тогда является (компактным) полиэдром, когда оно представляет собой объединение (конечного) семейства выпуклых многогранников. Любой полиэдр может быть представлен в виде объединения симплексов, пересекающихся только по целым граням. Такое представление называют триангуляцией полиэдра. Каждая триангуляция однозначно определена её симплициальной схемой, то есть множеством всех её вершин, в котором отмечены подмножества, являющиеся множествами вершин симплексов. Поэтому вместо полиэдров можно рассматривать лишь симп-лициальные схемы их триангуляций. Например, по симплициальной схеме можно вычислять группы гомологий и когомологий. Это делается следующим образом:
тогда и только тогда является (компактным) полиэдром, когда оно представляет собой объединение (конечного) семейства выпуклых многогранников. Любой полиэдр может быть представлен в виде объединения симплексов, пересекающихся только по целым граням. Такое представление называют триангуляцией полиэдра. Каждая триангуляция однозначно определена её симплициальной схемой, то есть множеством всех её вершин, в котором отмечены подмножества, являющиеся множествами вершин симплексов. Поэтому вместо полиэдров можно рассматривать лишь симп-лициальные схемы их триангуляций. Например, по симплициальной схеме можно вычислять группы гомологий и когомологий. Это делается следующим образом:
а) симплекс, вершины которого определённым образом упорядочены, называется упорядоченным симплексом данной триангуляции (или симплициальной схемы) К; формальные линейные комбинации упорядоченных симплексов данной размерности n с коэффициентами из данной группы G называются n-мepными цепями; все они естественным образом составляют группу, которая обозначается символом C n(K; G);
б) выбросив из упорядоченного n-мерного симплекса s вершину с номером i, 0 £ i £ n, получим упорядоченный (n—1)-мерный симплекс, который обозначается символом s(i); цепь 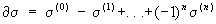 называется границей s; по линейности отображение
называется границей s; по линейности отображение 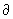 распространяется до гомоморфизма
распространяется до гомоморфизма 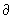 : Cn(K; G) ® Cn-1 (K; G);
: Cn(K; G) ® Cn-1 (K; G);
в) цепи с, для которых 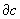 = 0, называются циклами, они составляют группу циклов Zn(K; G);
= 0, называются циклами, они составляют группу циклов Zn(K; G);
г) цепи вида  называются границами, они составляют группу границ Bn(K; G);
называются границами, они составляют группу границ Bn(K; G);
д) доказывается, что Bn(K; G) Ì Zn(K; G) (граница является циклом); поэтому определена факторгруппа
Hn(K; G) = Zn(K; G)/ Bn(K; G).
Оказывается, что группа Hn(K; G) изоморфна группе гомологий Hn(X; G) полиэдра X, триангуляцией которого является К. Аналогичная конструкция, в которой исходят не из цепей, а из коцепей (произвольных функций, определённых на множестве всех упорядоченных симплексов и принимающих значения в G ), даёт группы когомологий.
С этой конструкции, изложенной здесь в несколько модифицированной форме, и началось по существу становление алгебраической Топология В первоначальной конструкции рассматривались так называемые ориентированные симплексы (классы упорядоченных симплексов, отличающихся чётными перестановками вершин). Эта конструкция развита и обобщена в самых разнообразных направлениях. В частности, её алгебраические аспекты дали начало так называемой гомологической алгебре.
Самым общим образом симплициальную схему можно определить как множество, в котором отмечены некоторые конечные подмножества («симплексы»), причём требуется, чтобы любое подмножество симплекса было снова симплексом. Такая симплициальная схема является симплициальной схемой триангуляции некоторого полиэдра тогда и только тогда, когда число элементов произвольного отмеченного подмножества не превосходит некоторого фиксированного числа. Впрочем, понятие полиэдра можно обобщить (получив так называемые «бесконечномерные полиэдры»), и тогда уже любая симплициальная схема будет схемой триангуляции некоторого полиэдра (называемого её геометрической реализацией).
Произвольному открытому покрытию {Ua} каждого топологического пространства Х можно сопоставить симплициальную схему, вершинами которой являются элементы Ua покрытия и подмножество которой тогда и только тогда отмечено, когда элементы покрытия, составляющие это подмножество, имеют непустое пересечение. Эта симплициальная схема (и соответствующий полиэдр) называемому нервом покрытия. Нервы всевозможных покрытий в определённом смысле аппроксимируют пространство Х и, исходя из их групп гомологий и когомологий, можно посредством соответствующего предельного перехода получать группы гомологий и когомологий самого X. Эта идея лежит в основе почти всех конструкций общей теории гомологий. Аппроксимация топологического пространства нервами его открытых покрытий играет важную роль и в общей Топология
5. Топология многообразий
Хаусдорфово паракомпактное топологическое пространство называется n-мерным топологическим многообразием, если оно «локально евклидово», то есть если каждая его точка обладает окрестностью (называемой координатной окрестностью, или картой), гомеоморфной топологическому пространству 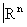 . В этой окрестности точки задаются n числами x1, …, xn, называемыми локальными координатами. В пересечении двух карт соответствующие локальные координаты выражаются друг через друга посредством некоторых функций, называемых функциями перехода. Эти функции задают гомеоморфизм открытых множеств в
. В этой окрестности точки задаются n числами x1, …, xn, называемыми локальными координатами. В пересечении двух карт соответствующие локальные координаты выражаются друг через друга посредством некоторых функций, называемых функциями перехода. Эти функции задают гомеоморфизм открытых множеств в 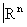 , называются гомеоморфизмом перехода.
, называются гомеоморфизмом перехода.
Условимся произвольный гомеоморфизм между открытыми множествами из 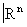 называть t-гомеоморфизмом. Гомеоморфизм, являющийся кусочно-линейным изоморфизмом, будем называть p-гомеоморфизмом, а если он выражается гладкими (дифференцируемыми любое число раз) функциями, — s-гомеоморфизмом.
называть t-гомеоморфизмом. Гомеоморфизм, являющийся кусочно-линейным изоморфизмом, будем называть p-гомеоморфизмом, а если он выражается гладкими (дифференцируемыми любое число раз) функциями, — s-гомеоморфизмом.
Пусть a = t, p или s. Топологическое многообразие называется a-многообразием, если выбрано такое его покрытие картами, что гомеоморфизмы перехода для любых его двух (пересекающихся) карт являются a-гомеоморфизмами. Такое покрытие задаёт a-структуру на топологическом многообразии X. Таким образом, t-многообразие — это просто любое топологическое многообразие, p-многообразия называются кусочно-линейными многообразиями. Каждое кусочно-линейное многообразие является полиэдром. В классе всех полиэдров n-мерные кусочно-линейные многообразия характеризуются тем, что любая их точка обладает окрестностью, кусочно-линейно изоморфной n-мерному кубу. s-многообразия называются гладкими (или дифференцируемыми) многообразиями. a-отображением a-многообразия называются называется при a = t произвольное непрерывное отображение, при a = s — произвольное кусочно-линейное отображение, при a = s — произвольное гладкое отображение, то есть непрерывное отображение, записывающееся в локальных координатах гладкими функциями. Взаимно однозначное a-отображение, обратное к которому также является a-отображением, называется a-гомеоморфизмом (при a = s также диффеоморфизмом), a-многообразия Х и Y называются a-гомеоморфными (при a = s — диффеоморфными), если существует хотя бы один a-гомеоморфизм X ® Y. Предметом теории a-многообразий является изучение a-многообразий и их a-отображений; при этом a-гомеоморфные a-многообразия считаются одинаковыми. Теория s-многообразий является частью кусочно-линейной Топология Теория s-многообразий называется также гладкой Топология
Основной метод современной теории многообразий состоит в сведении её задач к проблемам алгебраических Топология для некоторых нужным образом сконструированных топологических пространств. Эта тесная связь теории многообразий с алгебраической Топология позволила, с одной стороны, решить много трудных геометрических проблем, а с другой — резко стимулировала развитие самой алгебраической Топология
Примерами гладких многообразий являются n-мерные поверхности в 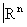 , не имеющие особых точек. Оказывается (теорема вложения), что любое гладкое многообразие диффеоморфно такой поверхности (при N ³ 2n + 1). Аналогичный результат верен и при a = t, p.
, не имеющие особых точек. Оказывается (теорема вложения), что любое гладкое многообразие диффеоморфно такой поверхности (при N ³ 2n + 1). Аналогичный результат верен и при a = t, p.
Каждое p-многообразие является t-многообразием. Оказывается, что на любом s-многообразии можно некоторым естественным образом ввести p-структуру (которая называется обычно у айтхедовской триангуляцией). Можно сказать, что любое a-многообразие, где a = p или s, является a’-многообразием, где a’ = t или p. Ответ на обратный вопрос: на каких a’-многообразиях можно ввести a-структуру (такое a’-многообразие при a’ = p называется сглаживаемым, а при a’ = t — триангулируемым), а если можно, то сколько? — зависит от размерности n.
Существует только два одномерных топологических многообразия: окружность S1 (компактное многообразие) и прямая линия 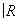 (некомпактное многообразие). Для любого a = p, s на t-многообразиях S1 и
(некомпактное многообразие). Для любого a = p, s на t-многообразиях S1 и 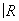 существует единственная a-структура.
существует единственная a-структура.
Аналогично, на любом двумерном топологическом многообразии (поверхности) существует единственная a-структура, и можно легко описать все компактные связные поверхности (некомпактные связные поверхности также могут быть описаны, но ответ получается более сложный). Для того чтобы поверхности были гомеоморфны, достаточно, чтобы они были гомотопически эквивалентны. При этом гомотопический тип любой поверхности однозначно характеризуется её группами гомологий. Существует два типа поверхностей: ориентируемые и неориентируемые. К числу ориентируемых принадлежит сфера S2 и тор T2. Пусть Х и Y — два связных n-мерных a-многообразия. Вырежем в Х и Y по шару (при n = 2 — диску) и склеим получившиеся граничные сферы (при n = 2 — окружности). При соблюдении некоторых само собой разумеющихся предосторожностей в результате снова получим a-многообразие. Оно называется связной суммой a-многообразий Х и Y и обозначается X#Y. Например, T2#T2 имеет вид кренделя. Сфера S n является нулём этого сложения, то есть S n#X = Х для любого X. В частности, S2#T2 = T2. Оказывается, что ориентируемая поверхность гомеоморфна связной сумме вида S2#T2#…#T2, число p слагаемых T2 называется родом поверхности. Для сферы p = 0, для тора p = 1 и т. д. Поверхность рода p можно наглядно представлять себе как сферу, к которой приклеено p «ручек». Каждая неориентируемая поверхность гомеоморфна связной сумме 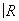 P2# ¼ #
P2# ¼ #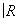 P2 некоторого числа проективных плоскостей
P2 некоторого числа проективных плоскостей 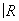 P2. Её можно представлять себе как сферу, к которой приклеено несколько Мебиуса листов.
P2. Её можно представлять себе как сферу, к которой приклеено несколько Мебиуса листов.
На каждом трёхмерном топологическом многообразии при любом a = p, s также существует единственная a-структура и можно описать все гомотопические типы трёхмерных топологических многообразий (однако групп гомологий для этого уже недостаточно). В то же время до сих пор (1976) не описаны все (хотя бы компактные связные) трёхмерные топологические многообразия данного гомотопического типа. Это не сделано даже для односвязных многообразий (все они гомотопически эквивалентны сфере S 3). Гипотеза Пуанкаре утверждает, что любое такое многообразие гомеоморфно S 3.
Для четырёхмерных (компактных и связных) топологических многообразий вопрос о существовании и единственности a-структур (a = p, s) ещё не решен, а их гомотопический тип описан только в предположении односвязности. Справедлив ли для них аналог гипотезы Пуанкаре, неизвестно.
Замечательно, что для компактных и связных топологических многообразий размерности n ³ 5 ситуация оказывается совсем иной: все основные задачи для них можно считать в принципе решенными (точнее, сведёнными к проблемам алгебраической Топология). Любое гладкое многообразие Х вкладывается как гладкая (n-мepная) поверхность в 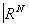 ; и касательные векторы к Х составляют некоторое новое гладкое многообразие TX, которое называется касательным расслоением гладкого многообразия X. Вообще, векторным расслоением над топологическим пространством Х называется топологическое пространство Е, для которого задано такое непрерывное отображение p : Е ® Х, что для каждой точки х Î Х прообраз v (слой) является векторным пространством и существует такое открытое покрытие {Ua} пространства X, что для любого a прообраз p—1(Ua) гомеоморфен произведению Ua ´
; и касательные векторы к Х составляют некоторое новое гладкое многообразие TX, которое называется касательным расслоением гладкого многообразия X. Вообще, векторным расслоением над топологическим пространством Х называется топологическое пространство Е, для которого задано такое непрерывное отображение p : Е ® Х, что для каждой точки х Î Х прообраз v (слой) является векторным пространством и существует такое открытое покрытие {Ua} пространства X, что для любого a прообраз p—1(Ua) гомеоморфен произведению Ua ´ 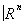 , причём существует гомеоморфизм p—1(Ua) ® Ua ´
, причём существует гомеоморфизм p—1(Ua) ® Ua ´ 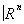 , линейно отображающий каждый слой p—1(x), x Î Ua, на векторное пространство {х} ´
, линейно отображающий каждый слой p—1(x), x Î Ua, на векторное пространство {х} ´ 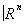 . При Е = TX непрерывное отображение p сопоставляет с каждым касательным вектором точку его касания, так что слоем p—1(x) будет пространство, касательное к Х в точке х. Оказывается, что любое векторное расслоение над компактным пространством Х определяет некоторый элемент группы KO(X). Таким образом, в частности, для любого гладкого, компактного и связного многообразия Х в группе KO(X) определён элемент, соответствующий касательному расслоению. Он называется тангенциальным инвариантом гладкого многообразия X. Имеется аналог этой конструкции для любого a. При a = p роль группы KO(X) играет некоторая другая группа, которая обозначается KPL(X), а при a = t роль этой группы играет группа, обозначаемая KTop(X). Каждое a-многообразие Х определяет в соответствующей группе [КО(Х), KPL(X) или KTop(X)] некоторый элемент, называемый его a-тангенциальным инвариантом. Имеются естественные гомоморфизмы KO(X) ® KPL(X) ® KTop(X), и оказывается, что на n-мерном (n ³ 5) компактном и связном a"-многообразии X, где a" = t, p, тогда и только тогда можно ввести a-структуру (a = р, если a" = t, и a = s, если a" = p), когда его a"-тангенциальный инвариант лежит в образе соответствующей группы [KPL(X) при a" = t и KO(X) при a" = p]. Число таких структур конечно и равно числу элементов некоторого фактормножества множества [X, Ya], где Ya — некоторое специальным образом сконструированное топологическое пространство (при a = s топологическое пространство Ya обозначается обычно символом PL/O, а при a = p — символом Top/PL). Тем самым вопрос о существовании и единственности a-структуры сводится к некоторой задаче теории гомотопий. Гомотопический тип топологического пространства PL/O довольно сложен и до сих пор (1976) полностью не вычислен; однако известно, что pi(PL/O) = 0 при i £ 6, откуда следует, что любое кусочно-линейное многообразие размерности n £ 7 сглаживаемо, а при n £ 6 единственным образом. Напротив, гомотопический тип топологического пространства Top/PL оказался удивительно простым: это пространство гомотопически эквивалентно K(ℤ2, 3). Следовательно, число кусочно-линейных структур на топологическом многообразии не превосходит числа элементов группы H 3(X, ℤ2). Такие структуры заведомо существуют, если H 4(X, ℤ2) = 0, но при H 4(X, ℤ2) ¹ 0 кусочно-линейной структуры может не существовать.
. При Е = TX непрерывное отображение p сопоставляет с каждым касательным вектором точку его касания, так что слоем p—1(x) будет пространство, касательное к Х в точке х. Оказывается, что любое векторное расслоение над компактным пространством Х определяет некоторый элемент группы KO(X). Таким образом, в частности, для любого гладкого, компактного и связного многообразия Х в группе KO(X) определён элемент, соответствующий касательному расслоению. Он называется тангенциальным инвариантом гладкого многообразия X. Имеется аналог этой конструкции для любого a. При a = p роль группы KO(X) играет некоторая другая группа, которая обозначается KPL(X), а при a = t роль этой группы играет группа, обозначаемая KTop(X). Каждое a-многообразие Х определяет в соответствующей группе [КО(Х), KPL(X) или KTop(X)] некоторый элемент, называемый его a-тангенциальным инвариантом. Имеются естественные гомоморфизмы KO(X) ® KPL(X) ® KTop(X), и оказывается, что на n-мерном (n ³ 5) компактном и связном a"-многообразии X, где a" = t, p, тогда и только тогда можно ввести a-структуру (a = р, если a" = t, и a = s, если a" = p), когда его a"-тангенциальный инвариант лежит в образе соответствующей группы [KPL(X) при a" = t и KO(X) при a" = p]. Число таких структур конечно и равно числу элементов некоторого фактормножества множества [X, Ya], где Ya — некоторое специальным образом сконструированное топологическое пространство (при a = s топологическое пространство Ya обозначается обычно символом PL/O, а при a = p — символом Top/PL). Тем самым вопрос о существовании и единственности a-структуры сводится к некоторой задаче теории гомотопий. Гомотопический тип топологического пространства PL/O довольно сложен и до сих пор (1976) полностью не вычислен; однако известно, что pi(PL/O) = 0 при i £ 6, откуда следует, что любое кусочно-линейное многообразие размерности n £ 7 сглаживаемо, а при n £ 6 единственным образом. Напротив, гомотопический тип топологического пространства Top/PL оказался удивительно простым: это пространство гомотопически эквивалентно K(ℤ2, 3). Следовательно, число кусочно-линейных структур на топологическом многообразии не превосходит числа элементов группы H 3(X, ℤ2). Такие структуры заведомо существуют, если H 4(X, ℤ2) = 0, но при H 4(X, ℤ2) ¹ 0 кусочно-линейной структуры может не существовать.
В частности, на сфере S n существует единственная кусочно-линейная структура. Гладких структур на сфере S n может быть много, например, на S 7 существует 28 различных гладких структур. На торе T n (топологических произведении n экземпляров окружности S 1) существует при n ³ 5 много различных кусочно-линейных структур, которые все допускают гладкую структуру. Таким образом, начиная с размерности 5, существуют гомеоморфные, но не диффеоморфные гладкие многообразия; сферы с таким свойством существуют, начиная с размерности 7.
Задачу описания (с точностью до a-гомеоморфизма) всех n-мерpных (n ³ 5) связных компактных a-многообразий естественно решать в два этапа: искать условия гомотопической эквивалентности a-многообразий и условия a-гомеоморфности гомотопически эквивалентных a-многообразий. Первая задача относится к гомотопической Топология и в её рамках может считаться полностью решенной. Вторая задача также по существу полностью решена (во всяком случае для односвязных a-многообразий). Основой её решения является перенос в высшие размерности техники «разложения на ручки». С помощью этой техники удаётся, например, доказать для n-мерных (n ³ 5) топологических многообразий гипотезу Пуанкаре (связное компактное топологическое многообразие, гомотопически эквивалентное сфере, гомеоморфно ей).
Наряду с a-многообразиями можно рассматривать так называемые a-многообразия с краем; они характеризуются тем, что окрестности некоторых их точек (составляющих край) a-гомеоморфны полупространству Xn ³ 0 пространства 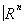 . Край является (n—1)-мерным a-многообразием (вообще говоря, несвязным). Два n-мерных компактных a-многообразия Х и Y называются (ко) бордантными, если существует такое (n+1)-мерное компактное a-многообразие с краем W, что его край является объединением непересекающихся гладких многообразий, a-гомеоморфных Х и У. Если отображения вложения X ® W и Y ® W являются гомотопическими эквивалентностями, то гладкие многообразия называются h-кобордантными. Методами разложения на ручки удаётся доказать, что при n ³ 5 односвязные компактные a-многоооразия a-гомеоморфны, если они h-кобордантны. Эта теорема о h-кобордизме доставляет сильнейший способ установления a-гомеоморфности a-многообразий (в частности, гипотеза Пуанкаре является её следствием). Аналогичный, но более сложный результат имеет место и для неодносвязных a-многообразий.
. Край является (n—1)-мерным a-многообразием (вообще говоря, несвязным). Два n-мерных компактных a-многообразия Х и Y называются (ко) бордантными, если существует такое (n+1)-мерное компактное a-многообразие с краем W, что его край является объединением непересекающихся гладких многообразий, a-гомеоморфных Х и У. Если отображения вложения X ® W и Y ® W являются гомотопическими эквивалентностями, то гладкие многообразия называются h-кобордантными. Методами разложения на ручки удаётся доказать, что при n ³ 5 односвязные компактные a-многоооразия a-гомеоморфны, если они h-кобордантны. Эта теорема о h-кобордизме доставляет сильнейший способ установления a-гомеоморфности a-многообразий (в частности, гипотеза Пуанкаре является её следствием). Аналогичный, но более сложный результат имеет место и для неодносвязных a-многообразий.
Совокупность 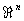 классов кобордантных компактных a-многообразий является по отношению к операции связной суммы коммутативной группой. Нулём этой группы служит класс a-многообразий, являющихся краями, то есть кобордантных нулю. Оказывается, что эта группа при a = s изоморфна гомотопической группе p2n+1MO (n+1) некоторого специально сконструированного топологического пространства MO (n+1), называется пространством Тома. Аналогичный результат имеет место и при a = p, t. Поэтому методы алгебраической Топология позволяют в принципе вычислить группу
классов кобордантных компактных a-многообразий является по отношению к операции связной суммы коммутативной группой. Нулём этой группы служит класс a-многообразий, являющихся краями, то есть кобордантных нулю. Оказывается, что эта группа при a = s изоморфна гомотопической группе p2n+1MO (n+1) некоторого специально сконструированного топологического пространства MO (n+1), называется пространством Тома. Аналогичный результат имеет место и при a = p, t. Поэтому методы алгебраической Топология позволяют в принципе вычислить группу 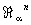 . В частности, оказывается, что группа
. В частности, оказывается, что группа 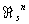 является прямой суммой групп ℤ2 в количестве, равном числу разбиений числа n на слагаемые, отличные от чисел вида 2m—1. Например,
является прямой суммой групп ℤ2 в количестве, равном числу разбиений числа n на слагаемые, отличные от чисел вида 2m—1. Например, 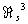 = 0 (так что каждое трёхмерное компактное гладкое многообразие является краем). Напротив,
= 0 (так что каждое трёхмерное компактное гладкое многообразие является краем). Напротив, 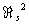 = ℤ2, так что существуют поверхности, кобордантные друг другу и не кобордантные нулю; такой поверхностью, например, является проективная плоскость
= ℤ2, так что существуют поверхности, кобордантные друг другу и не кобордантные нулю; такой поверхностью, например, является проективная плоскость 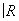 P 2.
P 2.
М. М. Постников.
6. Основные этапы развития топологии
Отдельные результаты топологического характера были получены ещё в 18—19 вв. (теорема Эйлера о выпуклых многогранниках, классификация поверхностей и теорема Жордана о том, что лежащая в плоскости простая замкнутая линия разбивает плоскость на две части). В начале 20 в. создаётся общее понятие пространства в Топология (метрическое — М. Фреше, топологическое — Ф. Хаусдорф), возникают первоначальные идеи теории размерности и доказываются простейшие теоремы о непрерывных отображениях (А. Лебег, Л. Брауэр), вводятся полиэдры (А. Пуанкаре) и определяются их так называемые числа Бетти. Первая четверть 20 в. завершается расцветом общей Топология и созданием московской топологической школы; закладываются основы общей теории размерности (П. С. Урысон); аксиоматике топологических пространств придаётся её современный вид (П. С. Александров); строится теория компактных пространств (Александров, Урысон) и доказывается теорема об их произведении (А. Н. Тихонов); впервые даются необходимые и достаточные условия метризуемости пространства (Александров, Урысон); вводится (Александров) понятие локально конечного покрытия [на основе которого в 1944 Ж. Дьёдонне (Франция) определил паракомпактные пространства]; вводятся вполне регулярные пространства (Тихонов); определяется понятие нерва и тем самым основывается общая теория гомологий (Александров). Под влиянием Э. Нётер числа Бетти осознаются как ранги групп гомологий, которые поэтому называются также группами Бетти. Л. С. Понтрягин, основываясь на своей теории характеров, доказывает законы двойственности для замкнутых множеств.
Во 2-й четверти 20 в. продолжается развитие общей Топология и теории гомологий: в развитие идей Тихонова А. Стоун (США) и Э. Чех вводят так называемое стоун — чеховское, или максимальное, (би)компактное расширение вполне регулярного пространства; определяются группы гомологий произвольных пространств (Чех), в группы когомологий (Дж. Александер, А. Н. Колмогоров) вводится умножение и строится кольцо когомологий. В это время в алгебраической Топология царят комбинаторные методы, основывающиеся на рассмотрении симплициальных схем; поэтому алгебраическая Топология иногда и до сих пор называется комбинаторной Топология Вводятся пространства близости и равномерные пространства. Начинает интенсивно развиваться теория гомотопий (Х. Хопф, Понтрягин); определяются гомотопические группы (В. Гуревич, США) и для их вычисления применяются соображения гладкой Топология (Понтрягин). Формулируются аксиомы групп гомологий и когомологий (Н. Стинрод и С. Эйленберг, США). Возникает теория расслоений (Х. Уитни, США; Понтрягин); вводятся клеточные пространства (Дж. Уайтхед, Великобритания).
Во 2-й половине 20 в. в СССР складывается советская школа общей Топология и теории гомологий: ведутся работы по теории размерности, проблеме метризации, теории (би)компактных расширений, общей теории непрерывных отображений (факторных, открытых, замкнутых), в частности теории абсолютов; теории так называемых кардинальнозначных инвариантов (А.В. Архангельский, Б. А. Пасынков, В. И. Пономарев, Е. Г. Скляренко, Ю. М. Смирнов и др.).
Усилиями ряда учёных (Ж. П. Серр и А. Картан во Франции, М. М. Постников в СССР, Уайтхед и др.) окончательно складывается теория гомотопий. В это время создаются крупные центры алгебраической Топология в США, Великобритании и др. странах; возобновляется интерес к геометрической Топология Создаётся теория векторных расслоений и К-функтора (М. Атья, Великобритания; Ф. Хирцебрух, ФРГ), алгебраическая Топология получает широкие применения в гладкой Топология (Р. Том, Франция) и алгебраической геометрии (Хирцебрух); развивается теория (ко)бордизмов (В. А. Рохлин, СССР; Том, С. П. Новиков) и теория сглаживания и триангулируемости (Дж. Милнор, США).
Развитие Топология продолжается во всех направлениях, а сфера её приложений непрерывно расширяется.
А. А. Мальцев.
Лит.: Александров П. С., Введение в общую теорию множеств и функций, М.—Л., 1948; Пархоменко А. С., Что такое линия, М., 1954; Понтрягин Л. С., Основы комбинаторной топологии, М.—Л., 1947; его же, Непрерывные группы, 3 изд., М., 1973; Милнор Дж., Уоллес А,, Дифференциальная топология. Начальный курс, пер. с англ., М., 1972; Стинрод Н., Чинн У., Первые понятия топологии, пер. с англ., М., 1967; Александров П. С., Комбинаторная топология, М.—Л., 1947; Александров П. С., Пасынков Б. А., Введение в теорию размерности. Введение в теорию топологических пространств и общую теорию размерности, М., 1973; Александров П. С., Введение в гомологическую теорию размерности и общую комбинаторную топологию, М., 1975; Архангельский А. В., Пономарев В. И,, Основы общей топологии в задачах и упражнениях, М., 1974; Постников М. М., Введение в теорию Морса, М., 1971; Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968; его же, Общая топология. Топологические группы. Числа и связанные с ними группы и пространства, пер. с франц., М., 1969; его же, Общая топология. Использование вещественных чисел в общей топологии. Функциональные пространства. Сводка результатов. Словарь, пер. с франц., М., 1975; Куратовский К., Топология, пер. с англ., т. 1—2, М., 1966—69; Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; Спеньер Э., Алгебраическая топология, пер. с англ., М., 1971.
М. М. Постников.
| "БСЭ" >> "Т" >> "ТО" >> "ТОП" |
Статья про "Топология" в Большой Советской Энциклопедии была прочитана 948 раз
| Пицца в сковороде |
| Коптим скумбрию дома в коробке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- Объединённая партия гаитянских коммунистов
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная