


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Корень (в математике)
Определение "Корень (в математике)" в Большой Советской Энциклопедии
Корень в математике, 1) Корень (в математике) степени n из числа а - число х (обозначаемое 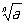 ), n-я степень которого равна а (то есть xn = а). Действие нахождения Корень (в математике) называют извлечением корня. При а ¹ 0 существует n различных значений Корень (в математике) (вообще говоря, комплексных); например, значениями
), n-я степень которого равна а (то есть xn = а). Действие нахождения Корень (в математике) называют извлечением корня. При а ¹ 0 существует n различных значений Корень (в математике) (вообще говоря, комплексных); например, значениями 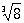 являются: 2; -1+i
являются: 2; -1+i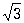 ; -1-i
; -1-i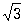 . К нахождению Корень (в математике) из чисел приводили различные геометрические задачи математиков глубокой древности. Среди вавилонских клинописных текстов (2-е тысячелетие до н. э.) имеются описания приближённого нахождения квадратного Корень (в математике) и таблицы квадратных Корень (в математике), а в египетских папирусах встречается для действия извлечения Корень (в математике) и особый знак. Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а
. К нахождению Корень (в математике) из чисел приводили различные геометрические задачи математиков глубокой древности. Среди вавилонских клинописных текстов (2-е тысячелетие до н. э.) имеются описания приближённого нахождения квадратного Корень (в математике) и таблицы квадратных Корень (в математике), а в египетских папирусах встречается для действия извлечения Корень (в математике) и особый знак. Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а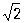 , если а - сторона), что позднее привело к открытию иррациональности. Ариабхата (5 в.) дал правила для извлечения квадратных и кубических Корень (в математике) Омар Хайям (2-я половина 11 - начало 12 вв.), аль-Каши (15 в.), немецкий математик М. Штифель (16 в.) извлекали Корень (в математике) высших степеней, исходя из формулы для (а+b) n. Л. Эйлер (18 в.) дал сохранившие своё значение до наших дней приближённые способы извлечения Корень (в математике) Квадратные К из отрицательных чисел, встречающиеся в 16 в. у Дж. Кардана и Р. Бомбелли, привели к открытию комплексных чисел.
, если а - сторона), что позднее привело к открытию иррациональности. Ариабхата (5 в.) дал правила для извлечения квадратных и кубических Корень (в математике) Омар Хайям (2-я половина 11 - начало 12 вв.), аль-Каши (15 в.), немецкий математик М. Штифель (16 в.) извлекали Корень (в математике) высших степеней, исходя из формулы для (а+b) n. Л. Эйлер (18 в.) дал сохранившие своё значение до наших дней приближённые способы извлечения Корень (в математике) Квадратные К из отрицательных чисел, встречающиеся в 16 в. у Дж. Кардана и Р. Бомбелли, привели к открытию комплексных чисел.
2) Корень (в математике) алгебраического уравнения
a0xn + a1xn-1+... + an-1x + an = 0 (1)
- число с, которое после подстановки его вместо х обращает уравнение в тождество. Корень (в математике) уравнения (1) называется также и Корень (в математике) многочлена
f (x) = a0xn + a1xn-1+... + an-1x + an.
Если с является Корень (в математике) многочлена f (x), то f (x) делится без остатка на х-с. См. также Многочлен, Уравнение.
| "БСЭ" >> "К" >> "КО" >> "КОР" >> "КОРЕ" |
Статья про "Корень (в математике)" в Большой Советской Энциклопедии была прочитана 706 раз
| Коптим скумбрию в коробке |
| Бургер двойного помола |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Японское море
- Периодическая система элементов
- Глициния
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Объединённая партия гаитянских коммунистов
- Сенсуализм
- «Сообразительный»
- Балкано-кавказская раса
- Навигация (морск.)
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Мандельштама - Бриллюэна рассеяние
- Кульчицкая Елена Львовна
- Театральные учебные заведения
- Электрическая постоянная